MathLinks 7 Student Centre

Course-Wide Content

Adapted Program

Please click here to access MathLinks 7 Adapted Program

To learn more about the book request an examination copy or contact your sales rep.

Games Web Links

The Fruit Game
	The Fruit Game is an interactive Nim-type game. Several kinds of fruit are placed on the "table". You may go first, or tell the computer to go first. You, or the computer, "eat" as many of one kind of fruit as you like per turn. The object is to beat the computer by removing the last piece of fruit from the table. ( http://www.2020tech.com/fruit/index.html )

Awari
	Awari is an ancient game based on mathematical principles. It was popular among poorer people because it can be played using stones and holes in the ground. You play against the computer, and have the option of moving first, or second. The object is to capture the greatest number of stones. ( http://members.aol.com/sstev74322/awari10.htm )

The Game of Life
	The game of life uses biological growth patterns as well as mathematical patterning to create a simulation of the growth or death of a culture. There are several rules for survival, which you can mix and match. The object is to create a living system that is able to sustain itself. ( http://www.math.com/students/wonders/life/life.html )

Hex-7
	Hex-7 is a strategy game that requires players to build a path across a playing surface made up of hexagons. You play against the computer and have the choice of first or second move. The game is offered at novice and advanced levels. ( http://www.mazeworks.com/hex7/index.htm )

Hare and Hounds
	Hare and Hounds is a strategy game popular in 19th century France among military officers. You can select hare or hounds. The hare must elude the hounds and escape. The hounds must trap the hare so that it cannot move. The game is offered at beginner and advanced levels. ( http://www.math.com/students/puzzles/hare/hare.html )

Rubik's Cube
	The Rubik's Cube applet allows you to manipulate a Rubik's Cube in three dimensions. The applet will randomly scramble the cube for you. ( http://www.javaonthebrain.com/java/rubik/ )

Gomoku
	Gomoku is a version of Tic Tac Toe that is played on an infinite game space and requires the winner to get five spheres in a row. You play against the computer. The game board is resizeable. ( http://www.checkers.ws/board_games/gomoku/gomoku_online.htm )

Sudoku
	Sudoku is a classic numbers game that requires you to complete a puzzle based on the integers 1 to 9. Once you have mastered the Easy level, you can proceed through Medium and Hard to Evil levels. ( http://www.websudoku.com/ )

Getting Started with TI-83 Plus/TI-84 Plus

These lessons provided by Texas Instruments will focus on introducing you to the TI-83 Plus and TI-84 Plus through various guided interactive activities.

These lessons are provided through Texas Instruments, and as such do not necessarily follow the Western and Northern Canadian Protocol The Common Curriculum Framework for Grades K–9 Mathematics. The following lessons and activities align with our curriculum and standards and we hope you take the time to enjoy the module and take from it what you feel will apply in your classroom setting.

Module 4: Draw on Your Knowledge of Coordinates
This module will examine the following:
• using graph window presets such as zstandard, zdecimal, zinterger, to create friendly viewing windows
• manually changing the window settings to create friendly viewing graph windows and manually setting the centre of a window
• graphing lines squares, circles using tools from the draw menu and clearing drawings
• drawing on the graph screen using the draw tools from the home screen and storing/recalling drawings
• downloading and using TI Connect to capture drawings on the home screen

Module 5: Transformations
This module will examine the following:
• using the set up editor and the alpha lock feature to name and create lists
• using graph window presets such as zoomstat and zsquare to create friendly viewing windows and manually changing window settings
• performing operations on lists to reflect, translate and dilate graphs
• using the augment and dim commands to change the size of lists

Module 8: Solving Equations
This module will examine the following:
• using the guess-and-test method to solve equations
• entering expressions and using concatenation on home screen to solve expressions
• entering functions using the y = editor and using the table feature to find missing values
• Solving Equations Algebraically store values and compare answers with expressions with rational numbers
• using y= editor to graphing and using the Calc menu to find intersection points
• expressing answers in fractional form

Module 17: Systems of Linear Equations
This module will examine the following:
• using home screen to guess and check solutions and to find the intersection point of two functions
• graphing functions and performing mathematical operations on functions in the y= editor
• entering matrices and finding a solution using the rref (row reduced echelon form) feature

To view these files, Adobe's free Flash Player application is required.

For additional support on this product and material please contact Texas Instruments.

For more exciting TI-83 Plus and TI-84 Plus modules, please visit the Texas Instruments site.

http://education.ti.com/educationportal/sites/US/nonProductMulti/pd_onlinealgebra_free.html

If you have a TI-Navigator system, please visit the Texas Instruments site for supporting modules.

http://education.ti.com/educationportal/sites/US/nonProductMulti/pd_onlinemgnavigator_free.html

The TI website offers a wide range of free activities for classroom use. Go to www.education.ti.com and visit the Activities Exchange portal for more resources that are aligned to Canadian standards.

* TI-83 Plus and TI-84 Plus are a trademark of Texas Instruments, Inc.
** TI-Navigator is a trademark of Texas Instruments, Inc.

Getting Started with TI-Nspire

These lessons provided by Texas Instruments will focus on introducing you to the TI-Nspire handheld by looking at the layout of the keypad and the key features of operating the Applications.

These lessons will focus on introducing you to the TI-Nspire handheld by looking at the layout of the keypad and the key features of operating the Applications.

Lesson 1
Familiarize yourself with the layout of the handheld keypad and how to navigate the various screens you will encounter.
Start this lesson

Lesson 2
Familiarize yourself with a few of the basics of the Graphs & Geometry application. You will learn how to graph and edit functions as well as edit the window settings using built-in zoom options.
Start this lesson

Lesson 3
The Basics of the Lists & Spreadsheet Application - Gain familiarity with all the basics of the Lists & Spreadsheet application. You will learn a variety of ways to enter values in to the spreadsheet.
Start this lesson

Lesson 4
Calculator, Notes, and the Document Model - Learn some basic features of the Notes application and Calculator application. The document model will also be discussed to help you see how the TI-Nspire can help students develop a deeper understanding of mathematical concepts through guided investigations.
Start this lesson

To view these files, Adobe's free Flash Player application is required.

Check out these exciting Texas Instruments web links:

Current TI online TI-Nspire^TM courses:

http://education.ti.com/educationportal/sites/US/sectionHome/tutorials.html

Current TI Online courses:

http://education.ti.com/educationportal/sites/US/sectionHome/pd_onlinecourses_free.html

Current Product Tutorials:

http://education.ti.com/educationportal/sites/US/sectionHome/tutorials.html

* TI-Nspire is a trademark of Texas Instruments, Inc.

Glossary

angle

The figure formed by two lines with a common endpoint called a vertex.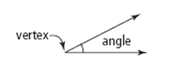

angle bisector

The line that divides an angle into two equal parts.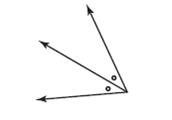

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta2_anglebisector.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (3.0K)</a>
(See page 95, Chapter 3.)

area

The number of square units contained in a two-dimensional region.

base (2-D geometry)

A side of a two-dimensional closed figure. Common symbol is b.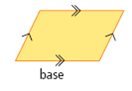

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta3_base.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (3.0K)</a>
(See page 101, Chapter 3.)

Cartesian plane

The plane formed when a horizontal number line and a vertical number line cross. Also called a coordinate grid.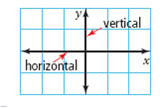

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta4_cartesianplane.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (5.0K)</a>
(See page 4, Chapter 1.)

central angle

An angle formed by two radii of a circle. The vertex of the angle is at the centre of the circle.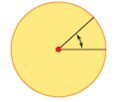

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta5_centralangle.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (4.0K)</a>
(See page 292, Chapter 8.)

circle

A set of points that are all the same distance from a fixed point called the centre.
(See page 266, Chapter 8.)

circle graph

A graph that represents data using sections of a circle.
(See page 287, Chapter 8.)

circumference

The distance around a circle. This is a linear measurement. Represented by the variable, C.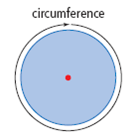

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta6_circumference.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (8.0K)</a>
(See page 274, Chapter 8.)

common denominator

A common multiple of the denominators of a set of fractions.

A common denominator for

and

is 6 because a common multiple of 2 and 3 is 6.

(See page 231, Chapter 7.)

common factor

A number that two or more numbers are divisible by.
4 is a common factor of 8 and 12.
(See page 203, Chapter 6.)

constant

A number that does not change. Increases or decreases the value of the expression no matter what the value of the variable.
In 2x + 4, the number 4 is the constant.
(See page 360, Chapter 10.)

coordinates

The values in an ordered pair (x, y).
(See page 5, Chapter 1.)

denominator

The number of equal parts in the whole or the group.

has a denominator of 4.

diameter

The distance across a circle through its centre. Represented by the variable, d.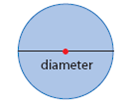

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta7_diameter.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (5.0K)</a>
(See page 269, Chapter 8.)

divisible

When a number can be divided by another number evenly, with no remainder.
(See page 199, Chapter 6.)

equally likely

Each outcome has the same chance of occurring.

equation

A mathematical statement with two expressions that have the same value.
3a – 21 = 4 and 2a = 6 – b are equations.
(See page 391, Chapter 11.)

equivalent fractions

Fractions that represent the same part of a whole or group.

and

are equivalent fractions.

estimate

To approximate an answer.
(See page 45, Chapter 2.)

experimental probability

The probability of an event occurring based on experimental results.
(See page 184, Chapter 5.)

exponent

The number of factors you multiply.
In the term 5², the number 2 is called an exponent.

expression

Any single number or variable, or a combination of operations involving numbers and variables.
2y - 7, 11x, and 14 are expressions.
(See page 358, Chapter 10.)

factors

Numbers that are multiplied to produce a product.

favourable outcome

A successful result in a probability experiment.
(See page 160, Chapter 5.)

fraction

A number that represents a part of a whole or a part of a group.

frequency table

A table used to show the number of occurrences in an experiment or survey.

graph

A visual way to show the relationship between two sets of numbers.
(See page 374, Chapter 10.)

height

The perpendicular distance from the base to the opposite side. Common symbol is h.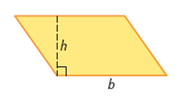

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta8_height.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (3.0K)</a>
(See page 101, Chapter 3.)

improper fraction

A fraction that has a numerator greater than the denominator, such as

(See page 246, Chapter 7.)

independent events

A result in which the outcome of one event has no effect on the outcome of another event.
(See page 166, Chapter 5.)

integer

Any of the numbers …, -3, -2, -1, 0, +1, +2, +3, ….

line

A set of points that contains no endpoints.

line segment

The part of a line between two endpoints.

linear relation

A pattern made by two sets of numbers that results in points along a straight line when graphed on a coordinate grid.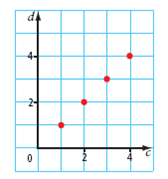

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta9_linearrelation.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (5.0K)</a>
(See page 372, Chapter 10.)

lowest terms

When the numerator and denominator of a fraction have no common factors other than 1.
(See page 204, Chapter 6.)

mean

The sum of a set of values divided by the number of values in the set.

6, 8, 5, 9, 12 Mean =
=	8

(See page 429, Chapter 12.)

measure of central tendency

A value that represents the centre of a set of data. It can be the mean, median, or mode.
(See page 423, Chapter 12.)

median

The middle number in a set of data after the data have been arranged in order.
For the data 2, 5, 6, 8, and 9, the median is 6.
For the data 1, 3, 7, 7, 9, and 10, the median is 7.
(See page 423, Chapter 12.)

mixed number

A number made up of a whole number and a fraction, such as

(See page 245, Chapter 7.)

mode

The most frequently occurring number in a set of data. There can be more than one mode.
For the data 3, 5, 7, 7, and 9, the mode is 7.
For the data 2, 2, 4, 6, 6, 8, and 11, the modes are 2 and 6.
(See page 423, Chapter 12.)

multiple

The product of a given number and a natural number like 1, 2, 3, and so on.
Some multiples of 3 are 3, 6, 9, 12, and 15.
(See page 232, Chapter 7.)

natural number

Any of the numbers 1, 2, 3, …

numerical coefficient

A number that multiplies the variable.
In 2x + 4, the number 2 is the numerical coefficient.
(See page 360, Chapter 10.)

numerator

The number of equal parts being considered in the whole or the group.

has numerator 3.

opposite integers

Two integers with the same numeral, but different signs. Two integers represented by points that are the same distance in opposite directions from zero on a number line.
+2 and -2 are opposite integers.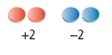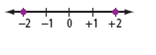

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta11_oppositeintegers.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (2.0K)</a>
(See page 311, Chapter 9.)

opposite operations

Operations that "undo" other operations. Some people call them "inverse operations."
Addition and subtraction are opposite operations.
Multiplication and division are opposite operations.
(See page 397, Chapter 11.)

order of operations

Correct sequence of steps for a calculation. Brackets first, then multiply and divide in order from left to right, and then add and subtract in order from left to right.
(See page 68, Chapter 2.)

ordered pair

A pair of numbers used to locate a point on a coordinate grid.

origin

The point where the x-axis and the y-axis cross.
(See page 5, Chapter 1.)

outcome

One possible result of a probability experiment.
(See page 160, Chapter 5.)

outlier

A value that is much smaller or larger than the other data values.
(See page 435, Chapter 12.)

overestimate

An estimate that is larger than the actual answer.
(See page 45, Chapter 2.)

parallel

Describes lines in the same plane that never cross or intersect.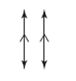

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta13_parallel.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a>
(See page 83, Chapter 3.)

parallelogram

A four-sided figure with opposite sides parallel and equal in length.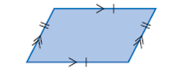

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta14_parallelogram.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (4.0K)</a>
(See page 100, Chapter 3.)

pattern

An arrangement of shapes, colours, numbers, letters, words, and so on, for which you can predict what comes next.
(See page 350, Chapter 10.)

percent

Means "out of 100" or "hundredths."

30% means 30 hundredths or 30 out of 100 or

or 0.30.

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta15_percent.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (4.0K)</a>
(See page 124, Chapter 4.)

perimeter

The distance around the outside of a two-dimensional shape or figure.

perpendicular

Describes lines that intersect at right angles (90⁰).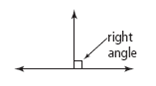

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta16_perpendicular.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (2.0K)</a>
(See page 83, Chapter 3.)

perpendicular bisector

A line that divides a line segment in half and is at right angles to it.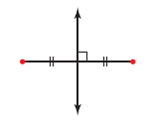

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta17_perpendicularbisector.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a>
(See page 90, Chapter 3.)

The ratio of the circumference of a circle to its diameter. The symbol for pi is ??.
(See page 274, Chapter 8.)

probability

The likelihood or chance of an event occurring. Probability can be expressed as a ratio, fraction, or percent.
(See page 158, Chapter 5.)

proper fraction

A fraction that has a numerator less than its denominator, such as

quadrants

The four regions on the coordinate grid.
(See page 5, Chapter 1.)

radius

The distance from the centre of a circle to the outside edge. Represented by the variable, r.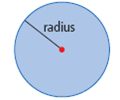

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta18_radius.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (5.0K)</a>
(See page 268, Chapter 8.)

random

An event in which every outcome has an equal chance of occurring.
(See page 171, Chapter 5.)

range

The difference between the largest and smallest values in a data set.
(See page 435, Chapter 12.)

reflection

A flip over a mirror line.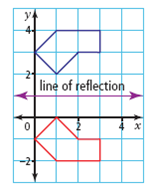

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta19_reflection.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (10.0K)</a>
(See page 19, Chapter 1.)

relationship

A pattern formed by 2 sets of numbers.
(See page 375, Chapter 10.)

repeating decimal

A decimal number with a digit or group of digits that repeats forever. Repeating digits are shown with a bar.

0.777… =

(See page 135, Chapter 4.)

rotation

A turn about a fixed point called the centre of rotation.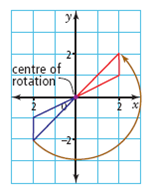

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta20_rotation.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (12.0K)</a>
(See page 19, Chapter 1.)

sample space

All possible outcomes of an experiment.
(See page 166, Chapter 5.)

sector

The section of a circle formed by two radii and an arc of the circle connecting the radii.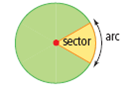

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta21_sector.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (6.0K)</a>
(See page 287, Chapter 8.)

semi-circle

Half of a circle.

table of values

A table showing two sets of related numbers.
(See page 367, Chapter 10.)

tally chart

A table used to record experimental results or data. Tally marks are used to count the data.

terminating decimal

A decimal number in which the digits stop.
0.4, 0.86, and 0.25 are terminating decimals.
(See page 136, Chapter 4.)

theoretical probability

The expected probability of an event occurring.
(See page 184, Chapter 5.)

transformation

Moves one geometric figure onto another. Examples are translations, reflections, and rotations.
(See page 18, Chapter 1.)

translation

A slide along a straight line.

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta22_translation.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (8.0K)</a>
(See page 18, Chapter 1.)

tree diagram

A diagram with a branch for each possible outcome of an event.
(See page 167, Chapter 5.)

underestimate

An estimate that is smaller than the actual answer.
(See page 45, Chapter 2.)

unit fraction

A fraction with a number of 1.

, etc.

value

A known or calculated amount.
(See page 360, Chapter 10.)

variable

A letter that represents an unknown number.
In 2x + 4, the letter x is the variable.
(See page 358, Chapter 10.)

vertex

A point where two sides of a figure meet. Plural is vertices.

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta23_vertex.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (3.0K)</a>
(See page 13, Chapter 1.)

whole number

Any of the numbers 0, 1, 2, 3, …

x-axis

The horizontal number line on the coordinate grid.
(See page 5, Chapter 1.)

x-coordinate

The first number in the ordered pair describing a point on a coordinate grid.
The x-coordinate of point P(2, 5) is 2.

y-axis

The vertical number line on the coordinate grid.
(See page 5, Chapter 1.)

y-coordinate

The second number in the ordered pair describing a point on a coordinate grid.
The y-coordinate of point P(2, 5) is 5.

zero pair

A pair of integer chips, with one chip representing +1 and one chip representing -1. The pair represents zero because (+1) + (-1) = 0.

<a onclick="window.open('/./olcweb/cgi/pluginpop.cgi?it=jpg::::/./olc2/dl/449925/mhr_ml7_ta24_zeropair.jpg','popWin', 'width=NaN,height=NaN,resizable,scrollbars');" href="#"><img valign="absmiddle" height="16" width="16" border="0" src="./olcweb/styles/shared/linkicons/image.gif"> (1.0K)</a>
(See page 310, Chapter 9.)

Project Ideas

Here are some interesting projects you might enjoy trying as you work through MathLinks 7. Do them alone or in a group.

To view these files, Adobe's free Acrobat Reader application is required.

Two-Dimensional Geometry (300.0K)

Simulations and Probability (295.0K)

Patterning (244.0K)

Data and Data Analysis (233.0K)

Circles (259.0K)

Master 8 Centimetre Grid Paper.pdf (15.0K)

Project Ideas Web Links

Circles Project #3 - Locate information on Blue Jays hitting stats
The Official Site of the Toronto Blue Jays Provides hitting, pitching, and fielding stats on players when fill last name of player into player locator box. Stats can be requested by playing season or training season.
( http://toronto.bluejays.mlb.com/stats/sortable_player_stats.jsp?c_id=torU )

Succeed in Math

Tips for Students
Why Studying Math is Different
Take Charge and Take Action
Preparing for Tests

Why Studying Math is Different

· Reading a math text is not like reading a novel. You may have to stop and think about some lines before proceeding.

· Math is a cumulative subject. If you miss a concept one day, it may come back to haunt you and could even prevent you from understanding concepts you study later. Always get help as soon as you recognize that you have a problem.

· Build up a network of math partners you can consult if you run into a roadblock. These are the days of easy communication. Telephone, email, and instant messaging are all available. Use them.

Take Charge and Take Action

· Take responsibility for your own success. If you find that you don't know or understand something, take whatever steps are necessary to fix the problem. Do not let others distract you from your purpose.

· Be an active participant in the classroom. Volunteer answers to questions and offer to place solutions on the blackboard. Ask questions immediately when you think you have lost the thread of the lesson.

· Math is learned by doing problems. Although you need to know some facts and procedures, you get really good at math by working through problems. It's wise to work on a problem yourself as much as possible. You may need to ask for help at some point, but don't give up too easily. The more you can do on your own, the more your brain will develop and the easier future problems will seem.

· Problem-solving is one of the key skills in the study of math. There are tips for problem-solving starting on page xiv in the front of MathLinks 7. Your teacher will show you additional strategies that you can use. In short, the steps are:
      – Understand the problem.
      – Plan how to solve it.
      – Do It! Carry out your plan.
      – Look Back. Review how you solved the problem and the answer you received. Does it make sense? If the answer seems unreasonable, it may be necessary to look for errors or select another strategy.

· Before beginning an assignment, review your class notes. Ensure that you understand the worked examples and the meaning of any new terms. Consider highlighting important concepts, equations, or definitions.

· As you work on each chapter, use the Foldables™ idea at the beginning of that chapter to keep track of information from the chapter, including key words, examples, key ideas, and what you need to work on.

· If you have completed the assigned problems, but still don't feel comfortable with the concepts, do a few more. Most teachers will assign about half of the problems in a given exercise. If you run out of practice questions before you feel comfortable with the concepts, ask the teacher for more. The MathLinks 7student site has many things to help you. Visit www.mathlinks7.ca and navigate to the student site to find additional resources.

· If you find that you need some help or a hint to proceed with the solution to a problem, be careful not to get too much help. You want a coach, not a handout. Once you see where to go, thank your coach. Don't ask for the entire solution. That robs you of an important learning opportunity.

· You have not failed at solving a question until you quit. Sometimes it is useful to skip a tricky question after thinking about it for a few minutes and then come back to it later.

· If there is any reason why you cannot finish your entire math assignment, it is better to do a few problems from each part than to do just the first problems in the assignment.

· If the homework load is light on a given day, use the extra time to review and practise concepts covered earlier in the course.

· Allow a few minutes at the end of your math work session to have a look at the next lesson so that you know what is coming up. It isn't necessary to work through the lesson, just to get a feeling for what is going to happen in the next math class.

Preparing for Tests

· If you do your homework conscientiously and work at fixing problems as they occur, then preparing for tests becomes much less difficult. All you need to do is remind yourself of the concepts that you are going to be tested on and do some sample problems to sharpen up your skills.

· When you receive your test, take a minute or two to look it over. You don't have to do question #1 first. If you see that you know how to attack question #3, then do that one first.

· Don't get bogged down on a question. If your strategy doesn't seem to be working and you are stuck for an alternative, go on to another question.

· Sometimes you will not finish a test in the time allotted. If this seems to be happening, do not panic. Accept that you are not going to finish. Make it your goal to do as many questions as you can before the time runs out.

· Read each question carefully. Be sure that you answer what was asked.

· Be sure to show your work. If you make an error and arrive at the wrong answer, you will at least get partial marks.

· If you have time left, use it to verify your answers. You can sometimes work backwards to do this. Alternatively, you can solve the same question a different way. Be sure to check calculations. A slip of the finger on a calculator can easily lead to a wrong answer.

· Watch out for panic attacks or "freezeups". This occasionally happens to a lot of students on a test. Time may be short, solutions are not going well, and you have an overwhelming sense of panic. The best thing to do is STOP. Turn the test over on your desk. Take several deep breaths, exhaling slowly. Remind yourself that you prepared for this test and that you can do most, probably all, of the questions on it. Then, return to the test, select a question that you can do, and work through it.

· If panic becomes a serious problem, consider learning one or more relaxation techniques or consulting a counsellor for other strategies. Keep in mind that these will not help if the real source of the panic is inadequate preparation for the test!

Web Links

Geometry of Transformations
	Having trouble visualizing transformations on paper? This site includes online, interactive applets that let you explore translations, rotations, and other transformations. Also included are interactive self-test quizzes, explanations, combinations of transformations, and extensions. ( http://www.mathsnet.net/transform/ )

Geometry From the Land of the Incas
	Geometry from the Land of the Incas contains geometry problems, illustrations, and historical references from Inca culture, including Cuzco, Macchu Picchu, the Nazca Lines, and even an Incan city on Mars. Resources include quizzes, crosswords, matching, and puzzles. ( http://agutie.homestead.com/files/index.html )

Fractions and Patterning
	This site features an on-line interactive applet for working with pattern blocks to investigate fractions and fractional relationships. Instructions can be read online or printed. ( http://www.arcytech.org/java/patterns/patterns_j.shtml )

Integers
	Need some practice in adding and subtracting integers using a number line to display the answer? This site includes problems at five different levels, from easy to "super brain". Each play receives instant feedback. Wrong answers are immediately corrected. ( http://www.funbrain.com/linejump/index.html )

Patterning and Equations
	Equation Match is a game in which the player is required to match equivalent equations in a grid arrangement. As each pair is correctly matched, a hidden picture is gradually revealed. The game offers sound and three levels of difficulty. ( http://www.bbc.co.uk/education/mathsfile/shockwave/games/equationmatch.html )

British Columbia Ministry of Education
	The British Columbia Ministry of Education site is an excellent general source for information on the educational system in British Columbia. ( http://www.bced.gov.bc.ca/students_ps.htm )

Alberta Ministry of Education
	The Alberta Ministry of Education site is an excellent general source for information on the educational system in Alberta. ( http://ednet.edc.gov.ab.ca/students/ )

Yukon Ministry of Education
	The Yukon Ministry of Education site is an excellent general source for information on the educational system in the Yukon. ( http://www.education.gov.yk.ca/ )

Northwest Territories Ministry of Education
	The Northwest Territories Ministry of Education site is an excellent general source for policy initiatives, curriculum, division of responsibilities and services, and other information on the educational system in Northwest Territories. ( http://www.gov.nt.ca/agendas/education/index.html )

Math Central
	Math Central is an Internet service for mathematics teachers and students from kindergarten to grade twelve. Included on the site is information about different mathematics careers, a question-and-answer forum, and a monthly mathematics problem. ( http://mathcentral.uregina.ca/ )

Learn Alberta Math Glossary
	This site offers a glossary of mathematical terms organized by grade level. Also offered are interactive applets geared to WNCP mathematics program. ( http://www.ronblond.com/MathGlossary/ )


The Math Forum (Drexel University)
	The Math Forum at Drexel University (Philadelphia, Pennsylvania) is a comprehensive site for students and teachers of mathematics. It includes problems of the week and the popular Ask Dr. Math question-and-answer forum. ( http://mathforum.org/ )



Mudd Math Fun Facts
	The Mudd Math site contains hundreds of interesting mathematics facts useful for adding interest to projects. The facts are organized by topic (algebra, geometry, probability, etc). Famous problems (the Birthday problem, colouring pizza slices, Devil's staircase, etc) are listed by name. ( http://www.math.hmc.edu/funfacts/ )



Fun Math Lessons
	Cynthia Lanius of Rice University (Houston, Texas) has created a number of mathematics lessons with an emphasis on having fun. Try them out. ( http://math.rice.edu/~lanius/Lessons/ )



Figure This! Math Challenges
	Supported by the NCTM, this site contains a large number of mathematics challenges you may enjoy. ( http://www.figurethis.org/index.html )



Coolmath 4 Kids
	The Coolmath site includes interactive math games, puzzles, fractals, geometry, and other interesting activities. Note: Because this is a commercially sponsored site, it includes advertising banners. ( http://www.coolmath4kids.com/ )


















Homework Help
	Need some help with your homework? This site offers worked examples, interactive self-quizzes, study tips, and test preparation, all organized by topics such as number sense, fractions, algebra, geometry, etc. ( http://www.math.com/students/homeworkhelp.html )



Tessellations
	This site offers activities and applets for creating and investigating tessellations online using pattern blocks. Tutorials, sample activities, and general information on tessellations and tiling are included. ( http://mathforum.org/sum95/suzanne/active.html )



Fermi Problems
	Looking for a fun way to practice estimation and real- world math? This library includes an explanation of what constitutes a Fermi problem, a short biography of Enrico Fermi, several worked examples, and a number of simple yet challenging Fermi questions. ( http://mathforum.org/workshops/sum96/interdisc/sheila1.html )



Career Profiles
	This link takes you to a number of career profiles of people who use mathematics in their jobs every day. Included are short biographies, educational qualifications, and practical uses for mathematics in the career. ( http://www.maa.org/careers/index.html )








Math is Fun
	This is a general site for all things mathematical. It includes games, puzzles, quizzes, worksheets, self tests, nets for polyhedra, and many other items. ( http://www.mathisfun.com/ )

Chapter 1

Student Book

Front Matter Student Book

Student Book (PDF)

Chapter 1 Student Book

Student Book (PDF)

Brain Teaser

Chapter 1 Coordinates and Design
Arrowheads

Consider this transformation sequence:
→ ↑ ↓
Which way does the next arrow in the sequence point?

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Three in a Row (2–4 Players)

Materials Needed:
• deck of standard playing cards
•

BLM: Three in a Row (16.0K)

1. Print BLM: Three in Row.

2. Use all aces through 9s in a standard deck of cards. The aces count as 1s. Red cards are negative, and black cards are positive.

3. Deal eight cards to each player. Place the remainder face down to be used as a draw pile.

4. The first player selects two cards from his or her hand to represent the coordinates of a point on the Cartesian grid.

• This point is marked on the grid using an initial or other symbol to identify the player.
• The two cards are placed in a discard pile, and the player draws two new cards.

5. Play moves clockwise. The next player takes a turn by playing a card and placing that number on the coordinate grid, then picking up a replacement card from the draw pile.

6. The first player to plot three points along the same line is the winner.

7. When all of the cards in the draw pile have been drawn, shuffle the discard pile and use it as the draw pile.

Notes:
a) Once a grid point is selected, no other player may select the same point.
b) It is not legal to place a point on one of the axes.

Web Links

Section 1.4, p. 31 Transformation Golf
Maths
	Go to Resources then scroll to the bottom to Transformation Golf ( http://www.subtangent.com/maths/index.php )

Chapter 2

Student Book

Chapter 2 Student Book

Student Book (PDF)

Brain Teaser

Chapter 2 Operations on Decimal Numbers
Double Digits

Fred has invited some of his classmates to his house on Water Street for an afternoon of video games. His house number is equal to double the sum of its digits. What address should they go to?

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Hit the Target (2 Players)
Materials Needed:

• deck of standard playing cards
• 4 coins
• scissors
•

BLM: Hit the Target (13.0K)

1. Print and cut out the four cards on BLM: Hit the Target.

2. Remove the queens, kings, and jokers from a pack of playing cards. • Aces represent 1s, and jacks represent 0s. • Other cards represent their face numbers. Use two coins per player as decimal points.

3. One player starts by dealing four playing cards to each player, and turning over one of the target cards.

4. Players use their four numbered cards and the two coins to form two decimal numbers. • The objective is to form two numbers with a product closest to the target card. • The player closest to the target card wins all 8 cards. • In case of a tie, players retrieve their own cards.

5. Play moves clockwise. For the second round, each player is dealt 4 new numbered cards and a new target card is turned over.

6. When all four target cards have been played, the game ends.

7. The player with the most playing cards at the end of the game is the winner.

Web Links

Section 2.2, p. 53 Sudoku Puzzles
Web Sudoku
	( http://show.websudoku.com/?level=1 )

Chapter 3

Student Book

Chapter 3 Student Book

Student Book (PDF)

Brain Teaser

Chapter 3 Geometry and Measurement
The Mysterious Figure

The grid lines shown are 1 cm apart. The area of the figure in square centimetres is a whole number. Determine the area.

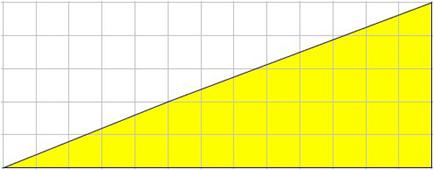Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Spin and Draw (Any Number of Players)

Materials Needed:

• 2 paper clips
• 2 pencils
• timer
•

BLM: Spin and Draw (16.0K)

1. Print the spinners on BLM: Spin and Draw. Use the paper clips and pencils to complete the spinners.

2. The first player spins the shape spinner and the spinner with numbers, which is the area spinner.
• This player then sketches that shape, showing a base and height that produce the required area.
• The second player times how long this takes.

3. If the other players agree that the shape and dimensions are correct, the player scores 100 points minus the number of seconds it took to finish the drawing.

4. Play moves clockwise. The player who just played is the timer for the next player.

5. If the same shape and area are spun during the same round, the player may not use the same dimensions that have already been used.

6. Continue until all players have had a turn.

7. In the second round, the numbers 1 and 2 may not be used as dimensions. Players who spin these areas must spin the area spinner again.

8. The first player to reach 500 points wins.

Web Links

Section 3.1, p. 88 Airport Design
Airport Taxi Diagrams
	( http://flighttraining.aopa.org/flight_bag/taxi_diagrams/ )

Section 3.2, p. 93 Airport Runways
Transport Canada
	To get info on runways, go to the official Transport Canada link. ( http://www.tc.gc.ca/CivilAviation/publications/tp312/Chapter3/3-1.htm )

Section 3.3, p. 99 Locating Runways
Virtual Skies
	The following link provides some practice in where to locate runways. ( http://virtualskies.arc.nasa.gov/design/design.htm )

Chapter 4

Student Book

Chapter 4 Student Book

Student Book (PDF)

Brain Teaser

Chapter 4 Fractions, Decimals, and Percents
Milky Way

Old Macdonald made a spreadsheet of his records for milk production. He found that, on average, 3.5 cows produce 3.5 pails of milk every 3.5 days. How many pails of milk can he expect from 7 cows in 7 days?

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Match and Win (2–4 Players)

Materials Needed:

• scissors
•

BLM: Match and Win (20.0K)

1. Print and cut out the 60 cards on BLM: Match and Win.

2. Shuffle and deal eight cards to each player. Place the remaining cards face down on the table.

3. Select a player to begin. The player may lay down any two cards that are equivalent.
Example: 0.5 is equivalent to ½ or 50%.
• If the rest of the players agree that the cards are equivalent, they are put aside, and the player scores 5 points.
• The player then draws one card from the pile, and must discard one.
• If a further match occurs, it may be put down and scored.

4. The next player continues in the same way, putting down any matches to score points. Players may pick up either the top card on the discard pile or from the face-down pile.

5. Play continues until one player runs out of cards. This player scores 5 bonus points. Players with cards still in their hands lose 2 points per card. No one may obtain a score of less than zero after any round.

6. Play continues until players reach a pre-determined score or until the end of a pre-determined time.

Web Links

Section 4.1, p. 131 History of Bubble Tea
Bubble Tea
	Bubble tea originated in Taiwan in the 1980s and was first sold in Canada in the 1990s. ( http://whatscookingamerica.net/BubbleTea.htm )

Chapter 5

Student Book

Chapter 5 Student Book

Student Book (PDF)

Brain Teaser

Chapter 5 Probability: Heads or Tails

"We'll each start with a coin and 24 counters," said Josef to Sunita. "You place your coin either heads up or tails up on the table and cover it with your hand so that I can’t see it. I’ll do the same. Then, we’ll both uncover our coins. If you have heads and I have tails, or vice-versa, I’ll give you two counters. If there are two heads, you give me one counter. If there are two tails, you give me three counters." Sunita thought about the probabilities of each outcome and decided that the game was fair. However, after playing for half an hour, she had lost all of her coins. Was the game fair? Explain.

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Roll and Collect (Any Number of Players)

Materials Needed:

• 11 counters per player (coins will work fine)
• 2 standard six-sided dice
• scissors
•

BLM: Roll and Collect (16.0K)

1. Print and cut out one counter board for each player from BLM: Roll and Collect.

2. Players arrange their 11 counters on their playing board any way they like. No more than 3 counters may be placed on any number.

3. The first player rolls a pair of dice, and removes any counters that have been placed on the sum rolled.

4. The next player takes a turn.

5. The player who first removes all counters from their playing board is the winner.

Web Links

Section 5.3, p. 171 Stories From Different Cultures Stories change over time as they are told and retold by different people. To find examples of stories from different cultures with math in them visit the links below.
Surlalune Fairy Tales
	( http://www.surlalunefairytales.com/goldilocks/history.html )



Mrs. Pohlmeyer's Kinder Page
	( http://www.mrspohlmeyerskinderpage.com/fairytales.htm )








FAIRY TALE MATH
	( http://www.lessonplanspage.com/MathArithmetic2up.htm )

Section 5.4, p. 177
The Game of Piggy
	( http://nrich.maths.org/public/viewer.php?obj_id=1258&part=index&refpage=topten )

Section 5.4, p. 178 The Game of Lahal A guessing game called Lahal involves six-player teams that hide sets of bones in their hands. To learn more about this game, played by Aboriginal people on the west coast of Canada follow the links below.
The Game of Lahal
	( http://secwepemc.sd73.bc.ca/sec_village/sec_lahal.html )



Simplified version of Lahal online
	( http://secwepemc.sd73.bc.ca/sec_village/Lahal_game.html )

Section 5.5, p. 189 Probability Experiments Computers are used in many different ways to study probabilities. For links to various probability experiments follow the links below.
Shodor Interactivate: Adjustable Spinner Activity
	( http://www.shodor.org/interactivate/activities/spinner/ )



Probability Simulations
	( http://www.mathsonline.co.uk/nonmembers/resource/prob/ )

Chapter 6

Student Book

Chapter 6 Student Book

Student Book (PDF)

Brain Teaser

Chapter 6 Introduction to Fraction Operations
Organizing a Sports Event

Sandor is organizing an international sports event. He finds that he can divide the participants into equal groups of 11 people. However, if he uses a smaller number of people, from 2 people to 10 people, he always has one person left over. What is the minimum number of people attending?

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Wholes Only (2–4 Players)

Materials Needed:

• scissors
•

BLM: Wholes Only (14.0K)

1. Print and cut out the fraction cards on BLM: Wholes Only.

2. Shuffle, and deal five fraction cards to each player. Place the rest face down in a pile.

3. Players inspect and arrange their cards.
• The object is to find groups of fractions that add to a whole number.
• The Wild Card may take on any fractional value between 0 and 1.

4. The first player places any group of cards that add to a whole number on the table, then draws a card. The next player does the same.

5. Play continues clockwise until all of the cards have been drawn, or one player lays down the last card from his/her hand.

6. Players score 20 points, minus the number of cards remaining in their hand.

7. Shuffle the cards and deal again. Play may continue for as many rounds as the players wish.

Web Links

Section 6.1, p. 201 The Number Zero Suggested URLs: For more information about the number zero see:
A history of Zero
	For more information about the number zero ( http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Zero.html )

Section 6.1, p. 203 Factoring and Venn Diagrams
Factoring and Venn diagrams
	( http://www.shodor.org/interactivate/student.html )

Chapter 7

Student Book

Chapter 7 Student Book

Student Book (PDF)

Brain Teaser

Chapter 7 Add and Subtract Fractions
Fraction Lineup

The first four fractions in a series are
Find the next four fractions.

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Sevens Down (2–4 Players)

Materials Needed:

• scissors
•

BLM: Sevens Down (14.0K)

1. Print and cut out the fraction cards on BLM: Sevens Down.

2. Shuffle, and deal the fraction cards evenly to all players. If any are left over, put them aside.

3. Players select a card and place it face up on the table.
• The player whose fraction has the greatest value collects all of the cards played and sets them aside.
• The Wild Card beats all other cards.

4. Play continues until all cards have been played.

5. Players total the value of the fractions on all cards that they have won, except the cards containing a seven in the numerator or denominator. These cards have a value of 0. The greatest total wins.

Web Links

Opener, p. 228 Eye of Horus





Great Scott!com
	Provides myth, visual of eye, explanation of fractions, and interactive visual that shows adding the fractions involved in the different parts of the eye. ( http://www.greatscott.com/hiero/eye.html )

Section 7.2, p. 239 Adding Fractions
Fractions-Adding
	( http://nlvm.usu.edu )

Chapter 7 Practice Test, p. 263 Fractions in Different Cultures For more information about fractions and mathematics in different cultures and different times follow the links below.
Babylonian and Egyptian fractions
	( http://nrich.maths.org/public/viewer.php?obj_id=2515&part=index&refpage=monthindex.php )



Egyptian fractions
	( http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fractions/egyptian.html )



Bibliography of books about math in different cultures
	( http://aleph0.clarku.edu/~djoyce/mathhist/numerals.html )

Chapter 8

Student Book

Chapter 8 Student Book

Student Book (PDF)

Brain Teaser

Chapter 8 Circles
Generations

Sylvia divided a circle in half. She then divided one piece in half again, and one of the smaller pieces in half again. She noticed that, if she placed herself in one of the smallest pieces, the circle graph represented the generations at a family gathering. Show how this worked on the circle graph.

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Circular Ashte Kashte (2–4 Players)

Materials Needed:
• 4 tokens per player (each player should have distinguishable tokens)
• 4 coins per group
•

BLM: Circular Ashte Kashte (31.0K)

Ashte Kashte is a racing game thought to have originated in India. A variant of the standard board is the circular board, consisting of a number of concentric circles. From 2 to 4 players begin on the coloured sectors. The object of the game is to reach the circle in the centre before anyone else.

1. Use the game board on BLM: Circular Ashte Kashte.

2. Players start on their starting sector. One at a time, they toss the four coins and move a token counterclockwise around the ring the number of spaces equal to the number of heads showing from their toss.

3. Play moves clockwise.
• On a second or subsequent turn, players may choose to start another token, or continue with the first token.
• Tokens move around the board until they have covered the first circle.
• They then move inwards to the next circle closer to the centre, and proceed counterclockwise.

4. Players who land a token on a sector occupied by an opponent’s piece capture the piece. The piece is removed from the board and has to start again.
• Pieces on a coloured sector cannot be landed on or captured.

5. Players who land on one of their own pieces create a double piece.
• Doubles may be moved together.
• Only other doubles can capture them.
• Doubles cannot be passed over, or jumped.

6. The middle circle may be entered only by a direct throw. If a player throws too high a number, another token must be moved, or the turn is forfeit.

7. The winner is the first player with all four tokens in the centre.

Web Links

Section 8.2, p. 278 Medicine Wheels





Medicine Wheels
	This website gives us information on the history, construction and meaning of Medicine Wheels. It tells us that medicine wheels are stone structures built by the natives of America and Canada for various spiritual and ritual purposes. Appearing mostly in Alberta, Canada, medicine wheels were built by laying out stones in a circular pattern that often looked like a wagon wheel laying on its side. The wheels could be large, reaching diameters of 75 feet. Although archeologists aren't exactly sure what each one was used for, it is thought that they probably had ceremonial or astronomical significance. ( http://www.crystalinks.com/medicinewheel.html )

Chapter 9

Student Book

Chapter 9 Student Book

Student Book (PDF)

Brain Teaser

Chapter 9 Add and Subtract Integers
Pet Store

The Chirp and Purr pet store sells only birds and cats. The store has eight animals, and the total number of legs they have is three times the total number of animals. How many birds and how many cats are in the store?

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Integer Race (Any Number of Players)

Materials Needed:
• 2 paperclips
• 2 pencils
• 1 counter per player
•

BLM: Integer Race (26.0K)

1. Print the spinners and game board on BLM: Integer Race. Use paper clips and pencils to complete the spinners.

2. Each player selects a counter and places it on Start.

3. Players spin the Integer spinner, and then the Sign spinner.
• The value of the Integer spinner indicates how many spaces may be moved.
• The Sign spinner indicates the direction of movement. Move clockwise for + and counterclockwise for –. Your Choice allows the player to select the direction.

4. Players who land on a space marked Lose a Turn, lose their next turn.
• Players who land on a space marked Your Choice, may choose the direction of their next move without using the Sign spinner.
• Players who land on a space marked Double Spin may have an extra turn.

5. The first player to complete one lap in either direction wins.

Web Links

page 308 Lacrosse Who developed the game of lacrosse? What was the game originally called?





Lacrosse
	( http://archives.cbc.ca/IDD-1-41-824/sports/lacrosse/ )

Section 9.2, p. 322 Canadian Hockey Players Canada has produced many famous hockey players. To learn more about famous Canadian hockey players follow the links.
Legends of Hockey
	( http://www.legendsofhockey.net )



ESPN
	Contemporary plus/minus statistics for individual players can be obtained on this site. ( http://sports.espn.go.com/nhl/players )



Brief history of hockey in aboriginal communities
	( http://www.collectionscanada.ca/hockey/kids/024003-2400-e.html )



Collections Canada
	( http://www.collectionscanada.ca/hockey/024002-2401-e.html )

Section 9.5, p. 336 Golf Terms What does an “albatross” mean in golf? What integer would you use to represent an albatross?
Golf Terms
	( http://www.scottishgolfhistory.net/origin_of_golf_terms.htm )



USGA
	( http://www.usga.org/questions/faqs/usga_history.html#1 )



Golf Dictionary
	( http://www.abc-of-golf.com/golf-dictionary.asp )

S

Chapter 10

Student Book

Chapter 10 Student Book

Student Book (PDF)

Brain Teaser

Chapter 10 Patterns and Expressions
Survival on Mars

While approaching for landing on Mars, the shuttlecraft’s engine malfunctioned and astronaut Jane Canuck was forced to land a 6-h walk from the nearest outpost. Jane knew that there was a radio transmitter at the outpost that she could use to call for help. The shuttlecraft had a supply of 1-h oxygen bottles, but Jane could only carry four at a time. How can Jane reach the outpost and call for help?

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Deduce the Digits (2 Players)

Materials Needed:
• pencil
• paper

1. Player 1 writes a 2-digit number on a piece of paper and turns it over so that Player 2 cannot see it.

2. Player 2 guesses a 2-digit number.
• If neither of the digits in Player 2’s number matches any digit in the hidden number, Player 1 must say “Miss.”
• If one of the digits guessed matches one of the digits in the hidden number, and it is in the correct decimal place, Player 1 must say “Hit.”
• If one of the digits guessed matches one of the digits in the hidden number, but it is in the wrong decimal place, Player 1 must say “Wing.”

3. Player 2 uses the results of the first guess to make a second guess. Play continues until Player 2 either guesses the number, or has made 8 unsuccessful guesses.

4. Players switch roles, and play again.

5. Points are awarded according to the table. The winner is the first player to reach or exceed 25 points.

Example:
Hidden number: 39
Player’s guess: 23

The digit 3 matches one of those in the hidden number, but is in the wrong decimal place. Award 1 wing.
Player takes 5 guesses to get the correct answer. Number of points earned: 6

Web Links

Section 10.1, p. 357 History of Calendars Research the history of calendars.





Calendars
	( http://webexhibits.org/calendars/year.html )

Chapter 11

Student Book

Chapter 11 Student Book

Student Book (PDF)

Brain Teaser

Chapter 11 Solving Equations
Cups and Squares

Marucia received a box of toonies from her uncle as a birthday present. She noticed that she could lay the toonies on a table in rows and columns to form a square, with none left over. If she divided the toonies into two equal piles, she could divide one pile evenly into three cups. What is the least number of toonies she could have received as a present?

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Cups and Counters (Any Number of Players)

Materials Needed:
• 6 plastic cups
• 24 plastic counters
• timer
• 2 standard six-sided dice

1. One at a time, players roll a die, and receive a number of plastic cups equal to the number rolled.
• They then roll two dice, add their values, add 12, and receive that number of counters.
• Players must model an equation by placing the same number of counters in each cup (at least one per cup) but allowing some counters outside the cup. The left side of the equation must equal the right side of the equation.
• Players have one minute to complete their equation.
• They earn 10 points for an equation that works.

2. Play moves clockwise until each player has had one turn.

3. On the second round, the time is reduced by 10 s. It is reduced by another 10 s on each of the following rounds.

4. The winner is the player with the most points after four rounds.

Example:
Each cup contains 3 counters.
The equation in the diagram works.
It represents:
2x + 4 = 10

Chapter 12

Student Book

Chapter 12 Student Book

Student Book (PDF)

Glossary Student Book

Student Book (PDF)

Index Student Book

Student Book (PDF)

Brain Teaser

Chapter 12 Working With Data
Three Siblings

"I am 12 years old," said Mustafa, "and am the middle child in a three-child family. My elder brother is 17. My age is both the mean and median of the three ages. How old is my younger sister?"

Click here for a hint

Click here for the solution

Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.

Crossword Puzzle

Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!

Student Games

Triple M Challenge (2–4 Players)

Materials Needed:
• deck of standard playing cards

1. Remove the jacks, queens, kings, and jokers from the deck of cards.

2. Each player is dealt 10 cards.

3. Players may elect to play the mean, the median, or the mode of the 10 cards in their hand. One minute is allowed for calculations.

4. The player with the highest number wins, and is awarded 12 points. If more than one player has the same highest number, the points are split among the tied players.

5. Shuffle the cards and deal again.

6. The first player to reach or exceed 50 points wins.