
| Bar graph | A graph that uses horizontal or vertical bars to represent data visually.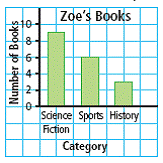 |
|||||||
| base of prism | Any face of a prism that reflects the general shape of the prism. (See page(s) 246) |
|||||||
| circle graph | A graph that represents data using sections of a circle. The sum of the percents in a circle graph is 100%.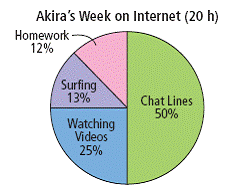 |
|||||||
| combined percents | Adding individual percents together. |
|||||||
| commutative property | The order of adding or multiplying quantities does not affect the result. a + b = b + a a x b = b x a |
|||||||
| constant | A number that does not change. |
|||||||
| cylinder | A three-dimensional object with two parallel and congruent circular bases.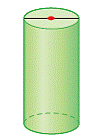 (See page(s) 182) |
|||||||
| distort | To change the appearance or twist the meaning of something in a way that is misleading. |
|||||||
| distributive property | Multiplication of each term inside the brackets of an expression by the term outside the brackets: a(b + c) = a x b + a x c = ab + ac |
|||||||
| double bar graph | A graph that uses two sets of horizontal or vertical bars to compare two sets of data across categories.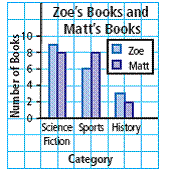 |
|||||||
| double line graph | A graph that uses two lines to represent changes of two sets of data over time.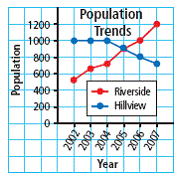 |
|||||||
| edge | A line segment where two faces meet.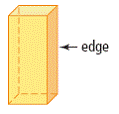 |
|||||||
| equation | A mathematical statement with two expressions that have the same value. The two expressions are separated by an equal sign. 3a – 2 = 4 is an equation. |
|||||||
| expression | Any single number, single variable, or combination of operations ( +, –, ×, ÷) involving numbers and variables. An expression does not include an equal sign. x + 9,
2y – 7, 8t, and 5 are expressions. |
|||||||
| face | A flat or curved surface.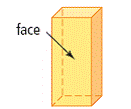 |
|||||||
| favourable outcome | A successful result in a probability experiment. |
|||||||
| formula | A mathematical statement that represents the relationship between specific quantities. An example is C = ?? × d, where C is the circumference and d is the diameter of a circle. |
|||||||
| fractional percent |
 (See page(s) 126) |
|||||||
| height | The perpendicular distance from the base to the opposite side. Common symbol is h.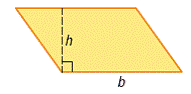 (See page(s) 246) |
|||||||
| hypotenuse | The longest side of a right angle triangle. Opposite the right angle. (See page(s) 89) |
|||||||
| improper fraction |
|
|||||||
| independent events | Results in which the outcome of one event has no effect on the outcome of another event. |
|||||||
| integer | Any of the numbers ..., –3, –2, –1, 0, 1, 2, 3, ... (See page(s) 410) |
|||||||
| interval | The spread between the smallest and the largest numbers in a range of numbers. (See page(s) 6) |
|||||||
| line graph | A graph that uses a line to represent changes in data over time.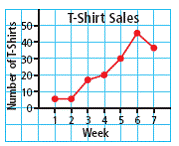 |
|||||||
| linear equation | An equation that, when graphed, results in points that lie along a straight line. (See page(s) 371) |
|||||||
| linear relation | A pattern made by a set of points that lie in a straight line.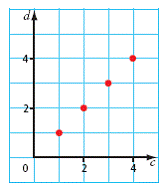 |
|||||||
| mixed number |
|
|||||||
| net | A two-dimensional figure, that, when folded, encloses a 3-D object.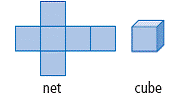 (See page(s) 170) |
|||||||
| numerical coefficient | A number that multiplies the variable. In 2x + 4, the number 2 is the numerical coefficient. |
|||||||
| opposite operation | A mathematical operation that undoes another operation. Subtraction and addition are opposite operations; multiplication and division are opposite operations. Also called inverse operation. |
|||||||
| order of operations | The correct sequence of steps for a calculation. Brackets first, then multiply and divide in order from left to right, and then add and subtract in order from left to right. |
|||||||
| orientation | The different position of an object formed by translating, rotating, or reflecting the object. (See page(s) 248) |
|||||||
| part-to-part ratio | Compare different parts of a group to each other. (See page(s) 48) |
|||||||
| part-to-whole ratio |
(See page(s) 48) |
|||||||
| percent |
 (See page(s) 122) |
|||||||
| perfect square | A number that is the product of two identical factors. It has an even number of prime factors. 2 × 2 = 4 is a perfect square. 2 × 2 × 3 × 3 = 36, so 36 is a perfect square. (See page(s) 82) |
|||||||
| pictograph | A graph that illustrates data using pictures and symbols.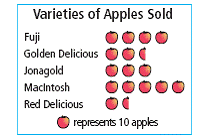 |
|||||||
| plane | A two-dimensional flat surface that extends in all directions. |
|||||||
| prime factorization | A number written as the product of its prime factors. The prime factorization of 6 is 2 × 3. (See page(s) 82) |
|||||||
| probability | The likelihood or chance of an event occurring. Probability can be expressed as a ration, a fraction, or a percent. (See page(s) 410) |
|||||||
| proper fraction |
|
|||||||
| proportion |
(See page(s) 64) |
|||||||
| Pythagorean relationship | The relationship between the lengths of the sides of a right triangle. The sum of the areas of the squares attached to the legs of the triangle equals the area of the square attached to the hypotenuse.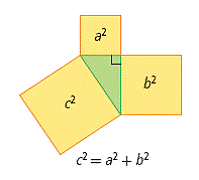 (See page(s) 90) |
|||||||
| rate | A comparison of two quantities measured in different units. $1.69 per 100 grams or $1.69/11 g is a rate for purchasing bulk food. 72 beats per minute or 72 beats/min is a heart rate. (See page(s) 55) |
|||||||
| reciprocal |
(See page(s) 224) |
|||||||
| rectangular prism | A prism whose bases are congruent rectangles.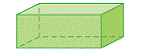 (See page(s) 170) |
|||||||
| right prism | A prism that has sides that are perpendicular to the bases of the prism. |
|||||||
| sample space | All possible outcomes of a probability experiment. (See page(s) 411) |
|||||||
| sign rules | In division, the quotient of two integers with the same sign is positive, and with different signs is negative. In multiplication, the product of two integers with the same sign is positive, and with different signs is negative. (See page(s) 294) |
|||||||
| square root | A number that when multiplied by itself equals a given value. The symbol is 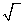 (See page(s) 83) |
|||||||
| surface area | The number of square units needed to cover a 3-D object. The sum of the areas of all the faces of an object.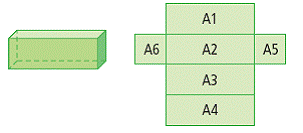 (See page(s) 177) |
|||||||
| table of values | A chart showing two sets of related numbers. |
|||||||
| tessellation | A pattern that covers an area or plane without overlapping or leaving gaps. Also called a tiling pattern.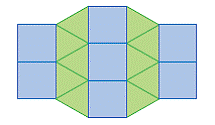 (See page(s) 446) |
|||||||
| three-term ratio | Compares three quantities measured in the same units. Can be written as a : b : c, or a to b to c. (See page(s) 47) |
|||||||
| tiling pattern | A pattern that covers an area or plane without overlapping or leaving gaps. Also called a tessellation. (See page(s) 446) |
|||||||
| tiling the plane | Using repeated congruent figures to cover an area without leaving gaps or overlapping. (See page(s) 446) |
|||||||
| transformation | A change in a figure that results in a different position or orientation. Examples are transformations, reflections, and rotations. (See page(s) 452) |
|||||||
| trend | The general direction in which a line graph is going. |
|||||||
| triangular prism | A prism with two triangular faces that are the same size and shape.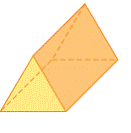 (See page(s) 172) |
|||||||
| two-term-ratio | Compares two quantities measured in the same units. Can be written as
a : b or a to b.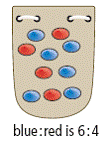 (See page(s) 47) |
|||||||
| unit price | A unit rate that involves prices. Often shown per 100 g or 100 mL. $5.00 per 100 g is a unit price. (See page(s) 58) |
|||||||
| unit rate | A rate in which the second term is 1. 64 beats/min is a unit rate. (See page(s) 56) |
|||||||
| variable | A letter that represents an unknown number. In 3a – 5, the variable is a. |
|||||||
| vertex | The point where three or more edges of a figure meet. The plural is vertices.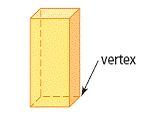 |
|||||||
| volume | The amount of space an object occupies. Measured in cubic units. (See page(s) 247) |
|||||||
| zero pair | A pair of integer chips with one chip representing +1 and one chip representing –1. The pair represents zero because (+1) + (–1) = 0. Any whole number of zero pairs represents zero.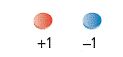 |
|||||||
|
Here are some interesting projects you might enjoy trying as you work through MathLinks 8 Adapted. Do them alone or in a group.
To do some of these projects, you may wish to use the special paper that has been provided online. Also, there are Web Links to help you access necessary information. Project Ideas Master Sheets |
|
Tips for Students Why Studying Math is Different · Reading math is not like reading a novel. You may have to stop and think about some lines before continuing. · It is important that you understand each concept you learn in math. If you miss a concept one day, you might not be able to understand concepts you study later. Get help if you do not understand something. · Make friends with people who can help you if you are having trouble understanding something. Get help on the telephone or by email or instant messaging. · Participate when you are in class. Answer questions and volunteer to write your answers on the blackboard. Ask questions if you are confused. · Math is learned by doing problems. You get really good at math by doing problems yourself. You might need to ask for help, but do as much as you can on your own. · Problem-solving is an important skill. There are tips for problem-solving on page xii of MathLinks 8 Adapted. The steps are: · Before you begin an assignment, look at your class notes. Make sure you understand the examples and any new words. · Use the Foldable at the beginning of each chapter to keep track of information. · If you have finished the assigned problems and still don’t feel comfortable with the concepts, do more questions. The MathLinks 8 Adapted student site has many things to help you. Go to www.mathlinks8.ca and follow the links to the student site to find more resources. · If you cannot finish your entire math assignment, it is better to do a few problems from each part than just the first problems in the assignment. · If you do not have very much homework, use the extra time to review and practise concepts you learned earlier in the year. · If you do your homework every day and make sure you understand concepts as you learn them, it is easier to study for tests. All you need to do is review the concepts you will be tested on and do some practice problems. · When you get your test, take a minute to look over it. You do not have to do question #1 first. If you know how to do question #3, do that one first. · Don’t get stumped by a question. If your strategy isn’t working, go to another question. · Sometimes you will not be able to finish a test in the amount of time given. Don’t panic. Do as many questions as you can. · Read each question carefully. Underline what the question is asking for. Make sure you answer what the question is asking. · Show your work. If you make a mistake, you will get some marks. |
|
Place It! | ||
| http://www.mathsisfun.com/games/place-it.html | ||
| This two-dimensional geometry game called Place It! tests your spatial sense by requiring you to assemble a square from odd-shaped pieces. The number of pieces can be varied to adjust the difficulty of the game. Players play against the clock to determine winners and losers. ( http://www.mathsisfun.com/games/place-it.html ) |
||
|
Mathematics and Computation: The Hydra Game | ||
| http://math.andrej.com/2008/02/02/the-hydra-game/ | ||
| Based on the creature from Greek mythology with many heads, the hydra, this is sometimes billed as “the game you can’t lose”. Although this claim refers only to the fact that every variation of the game has a solution, there is a fair amount of strategy involved in determining the solution in a minimum number of steps, allowing for competition among players. Winning strategies require good number sense, and will sharpen your numerical skills. ( http://math.andrej.com/2008/02/02/the-hydra-game/ ) |
||
|
Let’s Make a Deal | ||
| http://math.ucsd.edu/~crypto/Monty/monty.html | ||
| Based on a popular television program, Let’s Make a Deal requires you to make a selection, and then, decide whether to switch your selection based on information provided by the computer. The strategy that helps you to win is based on probability, and can be deduced using tools that you learn in this course. ( http://math.ucsd.edu/~crypto/Monty/monty.html ) |
||
|
Playing With JAVA: The Chomp Game | ||
| http://lpcs.math.msu.su/~pentus/abacus.htm | ||
| In an unusual twist, the first step in The Chomp Game requires you to deduce the rules. Once you have done so, you can play the game. Any number can play. ( http://lpcs.math.msu.su/~pentus/abacus.htm ) |
||
|
Linear Lasers | ||
| http://mathforum.org/te/exchange/hosted/linearlasers/ | ||
| Polish your skills at visualizing linear relations in the context of a game. Given two targets, you must correctly construct the linear equation that will hit both targets. ( http://mathforum.org/te/exchange/hosted/linearlasers/ ) |
||
|
Factor Game | ||
| http://illuminations.nctm.org/ActivityDetail.aspx?ID=12 | ||
| Need some practice before tackling fraction operations? The Factor Game allows two players to compete against each other while brushing up on factoring skills needed for a variety of mathematics topics, including fraction operations. You can also play against the computer. ( http://illuminations.nctm.org/ActivityDetail.aspx?ID=12 ) |
||
|
The All New & Improved Fruit Game! | ||
| http://www.2020tech.com/fruit/index.html | ||
| The Fruit Game is an interactive Nim-type game. Several kinds of fruit are placed on the table. You may go first, or tell the computer to go first. You, or the computer, “eat” as many of one kind of fruit as you like per turn. The object is to beat the computer by removing the last piece of fruit from the table. ( http://www.2020tech.com/fruit/index.html ) |
||
|
Klondinski’s Nim Engine | ||
| http://www.chlond.demon.co.uk/Nim.html | ||
| This is a version of the Nim game. ( http://www.chlond.demon.co.uk/Nim.html ) |
||
|
Tower of Hanoi | ||
| http://www.cut-the-knot.org/recurrence/hanoi.shtml | ||
| The Tower of Hanoi puzzle was invented in 1883 by the French mathematician, Edouard Lucas. A (variable) number of rings are placed in a tower, largest to smallest. The object is to move the rings, one at a time, onto two additional towers, until all of the rings are on the last tower. It is not permitted to have a larger ring on top of a smaller one. ( http://www.cut-the-knot.org/recurrence/hanoi.shtml ) |
||
|
Hammurabi–Long Live the King! | ||
| http://maddrio.com/hammurabi/hammurabi.php | ||
| Hammurabi is a game based on the Babylonian King, Hammurabi who is credited with the first code of law. You are placed in charge of the kingdom for ten years and must make economic decisions each year of your reign. The computer calculates the results of your decisions, along with some random factors that you cannot control. The objective is to end your reign with the kingdom in a better state than when you started. ( http://maddrio.com/hammurabi/hammurabi.php ) |
||
|
Basic Skills Resources: Awari | ||
| http://members.aol.com/sstev74322/awari10.htm | ||
| Awari is an ancient game based on mathematical principles. It was popular among poorer people because it can be played using stones and holes in the ground. You play against the computer, and have the option of moving first or second. The object is to capture the greatest number of stones. ( http://members.aol.com/sstev74322/awari10.htm ) |
||
|
Lunar Lander | ||
| http://www.frontiernet.net/~imaging/lunar_lander_game.html | ||
| Lunar Lander tests your ability to monitor rates of change while you bring a spacecraft to a safe landing before your fuel runs out. You can land on Earth, the moon, Mars, or Neptune to investigate the effects of different gravitational fields ( http://www.frontiernet.net/~imaging/lunar_lander_game.html ) |
||
|
Pentominoes | ||
| http://www.math.clemson.edu/~rsimms/java/pentominoes/ | ||
| Pentominoes are made up of five squares in different combinations to form a variety of shapes. The object of the game is to tile a section of the plane with no empty squares left over. You can rotate or flip any pentomino before placing it in the playing area. ( http://www.math.clemson.edu/~rsimms/java/pentominoes/ ) |
||
|
The Chaos Game | ||
| http://math.bu.edu/DYSYS/applets/chaos-game.html | ||
| The Chaos Game makes use of the Sierpinski Triangle and some of the Chaos Theory behind the generation of fractals to present a challenging puzzle. There are four levels of difficulty provided. ( http://math.bu.edu/DYSYS/applets/chaos-game.html ) |
||
|
What is the Game of Life? | ||
| http://www.math.com/students/wonders/life/life.html | ||
| The Game of Life uses biological growth patterns as well as mathematical patterning to create a simulation of the growth or death of a culture. There are several rules for survival, which you can mix and match. The object is to create a living system that is able to sustain itself. ( http://www.math.com/students/wonders/life/life.html ) |
||
|
Hex-7 | ||
| http://www.mazeworks.com/hex7/index.htm | ||
| Hex-7 is a strategy game that requires players to build a path across a playing surface made up of hexagons. You play against the computer and have the choice of first or second move. The game is offered at novice and advanced levels. ( http://www.mazeworks.com/hex7/index.htm ) |
||
|
Hare and Hounds | ||
| http://www.math.com/students/puzzles/hare/hare.html | ||
| Hare and Hounds is a strategy game that was popular among military officers in France during the 1800s. You can select hare or hounds. The hare must elude the hounds and escape. The hounds must trap the hare so that it cannot move. The game is offered at beginner and advanced levels. ( http://www.math.com/students/puzzles/hare/hare.html ) |
||
|
Sliding Tile Game | ||
| http://www.squarefree.com/15game.html | ||
| The Sliding Tile Game is a version of the classic game played with 16 spaces, one of which is empty. You must slide the remaining tiles, using the empty space, to reassemble a picture. This version allows you to slide more than one tile at a time. ( http://www.squarefree.com/15game.html ) |
||
|
Hidden Picture | ||
| http://www.aplusmath.com/cgi-bin/games/geopicture | ||
| This is a variation of a memory game. You must correctly identify geometric terms to reveal pieces of a hidden picture. Several pictures are available. ( http://www.aplusmath.com/cgi-bin/games/geopicture ) |
||
|
Jigsaw Puzzle Size-Up | ||
| http://pbskids.org/cyberchase/games/sizeandscale/sizeandscale.html | ||
| This is a variant on an electronic jigsaw puzzle in which you need to make each piece larger or smaller by one of six available factors, before you can add it to the puzzle. To make things trickier, you have only a limited amount of time to determine the correct size for each piece. ( http://pbskids.org/cyberchase/games/sizeandscale/sizeandscale.html ) |
||
|
Rubik Unbound | ||
| http://www.javaonthebrain.com/java/rubik/ | ||
| The applet allows you to manipulate a Rubik’s cube in three dimensions. The applet will randomly scramble the cube for you. ( http://www.javaonthebrain.com/java/rubik/ ) |
||
|
Gomoku Board Game Online | ||
| http://www.checkers.ws/board_games/gomoku/gomoku_online.htm | ||
| Gomoku is a version of Tic Tac Toe that is played on an infinite game space and requires the winner to get five spheres in a row. You play against the computer. The game board can be resized. ( http://www.checkers.ws/board_games/gomoku/gomoku_online.htm ) |
||
|
Web Sudoku | ||
| http://www.websudoku.com/ | ||
| Sudoku is a classic numbers game that requires you to complete a puzzle using the integers 1 to 9. Once you have mastered the Easy level, you can proceed through Medium and Hard to Evil levels. ( http://www.websudoku.com/ ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Line ’Em Up (2–4 Players) Materials Needed: • small counters in a different colour per player • one eight-sided die and one twelve-sided die • 1. Print the game board on BLM: Line ’Em Up. 2. Distribute counters to each player. 3. The first player rolls the twelve-sided die to determine an x-coordinate and then the eight-sided die to determine a y-coordinate. The player places the counter on the appropriate point on the playing board. 4. Play moves to the next player who rolls the dice and places a counter on the game board. Play continues clockwise. Note: More than one counter may occupy a point on the playing board. If this happens, stack the counters on the point. 5. Players continue rolling the dice until the end of the round. The round ends when a player has three counters that show a linear relationship, forming a straight line diagonally, horizontally, or vertically. 6. The first player to identify the linear relationship wins the round and receives 1 point. The counters are cleared off the board for the next round. Play continues for as many rounds as players wish. 7. The winner is the player with the highest number of points. |
| USATODAY.com | ||
| Provides data about the 20 top-selling digital tracks with their corresponding rank on the year-end national airplay and mastertone charts. ( http://www.usatoday.com/life/music/news/2007-01-04-music-sales-side_x.htm ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
At Any Ratio (2–4 Players) Materials Needed: • deck of playing cards • two twelve-sided dice 1. Remove the kings from the deck of cards. One player deals the remaining cards equally to each player. • Aces represent 1s, jacks represent 11s, and queens represent 12s. • Other cards represent their face numbers. 2. Each player begins with 10 points. Each player rolls one die to decide who will play first. The player with the highest roll goes first. If there is a tie, roll again. 3. The first player rolls the two dice and determines the ratio between the two numbers rolled. The player looks for cards in his or her hand that form an equivalent ratio in lowest terms. Any cards that show the same ratio in lowest terms are placed on the table. Example: Sunita rolls the ratio 8 : 12. She has a 2 and a 3 in her hand. This is the ratio of 8 : 12 expressed in lowest terms. She puts the 2 and the 3 on the table. 4. The other players check the cards on the table. If the ratio is correct and is in lowest terms, the player is awarded 1 point. If the ratio is incorrect, or is not in lowest terms, the player loses 1 point. 5. Play moves to the next player. Play ends when one player runs out of cards or after an agreed upon time limit. The winner is the player with the most points at the end of the game. |
|
SE page 45 Information about Folklorama® | ||
| Folk Arts Council of Winnipeg | ||
| Provides news articles and a calendar of events. ( http://www.folklorama.ca/ ) |
||
|
SE page 53 Practise solving ratio problems | ||
| National Council of Teachers of Mathematics | ||
| Provides several ratio problems. ( http://www.figurethis.org/challenges/c25/challenge.htm ) |
||
|
SE page 54 Information about the golden ratio in nature, architecture, art, poetry, and music | ||
| Queen’s University Faculty of Education | ||
| Information and visuals about the golden ratio in architecture including The Parthenon and the Great Pyramids of Giza. ( http://educ.queensu.ca/~fmc/october2001/GoldenArc.htm ) |
||
| University of Georgia | ||
| This site was developed by J. Wilson.
Information about the golden ratio including a brief history, definitions, golden geometry, and the golden ratio in art and architecture. ( http://jwilson.coe.uga.edu/EMT668/EMAT6680.2000/Obara/Emat6690/Golden%20Ratio/golden.html ) |
||
| Department of Mathematics, Surrey University, Guildford, UK | ||
| This site was developed by R. Knott.
Information about the golden ratio in architecture, art, and music. Includes a Things to Do investigation about logos that are golden rectangles and numerous active links. ( http://www.mcs.surrey.ac.uk/Personal/R.Knott/Fibonacci/fibInArt.html ) |
||
|
SE page 73 International food recipes | ||
| CooksRecipes.com | ||
| Provides recipes by category and by country or region. ( http://www.cooksrecipes.com/category/international.html ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Square Cuts (Any Number of Players) Materials Needed: • sheet of paper per player • ruler per player • scissors per pair of players • coloured pencils • timer 1. On a sheet of paper, each player draws a right triangle of any size. A square is drawn on each of the two sides and the hypotenuse of the triangle. The squares are cut out and the right triangle is set aside. 2. Divide each square into five shapes by drawing straight lines. Each shape is coloured such that no two touching shapes are the same colour. 3. Cut out the coloured shapes by cutting along the lines, mix up the shapes, and pass the shapes to the player on the right. 4. Start the timer. Each player needs to reassemble the shapes back into the original squares such that the squares form the sides of a right triangle. Each player records the time it took to reassemble the original squares. Stop the timer when all players are done. 5. The score for each player is 300 – t, where t is the time required to reassemble the shapes, in seconds. 6. The winner is the player with the highest score. |
|
SE page 79 Information about the game of Playing Leader | ||
| NativeTech | ||
| Native American Technology and Art
Provides a description and a visual of the game. ( http://www.nativetech.org/games/boardgames.html ) |
||
|
SE page 91 Explore the Pythagorean relationship | ||
| Mission: Algebra | ||
| Use a set of tangrams to model the Pythagorean relationship. Scroll down on the right to Tangram Model and choose Click to Enlarge. ( http://neirtec.terc.edu/ma/examples/07_example_p01.cfm?fromPage=examples/00_toc.cfm&fr... ) |
||
| Mission: Algebra | ||
| Explore nine interactive proofs for the Pythagorean Theorem. ( http://www.ies.co.jp/math/java/geo/pythagoras.html ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Nail the Percent (2–4 Players) Materials Needed: • two paper clips • two pencils • timer • calculator • 1. Print and cut out the spinners on BLM: Spinners. Use the paper clips and pencils to complete the spinners. 2. The first player spins both spinners. The player to the left starts the timer. 3. The first player places the smallest number spun over the largest number to form a fraction. If the numbers are equal, place either one over the other. If two zeroes are spun, the player receives 5 points, and play moves to the next player. 4. The player has 10 s to estimate the percent that is equivalent to the fraction. Points are awarded according to the table. 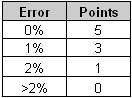 Example: The fraction is 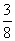 5. Play moves to the next player. The player to the left is the timer. 6. End the game after 20 rounds. The winner is the player with the highest score. |
|
SE page 143 Data and tips about conserving water | ||
| American Water Works Association | ||
| Provides conservation tips at home. From the list on the left, click on Conservation Outside for outdoor conservation tips and click on Water Use Statistics for data about water use. ( http://www.drinktap.org/consumerdnn/Default.aspx?tabid=83 ) |
||
|
SE page 145 PST rates by province | ||
| Taxtips.ca | ||
| Provides information about PST rates by province or territory. Use the active links for more information about provinces that charge PST. ( http://www.taxtips.ca/pst/pstrates.htm ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Para Lelli Pipe Ed (Pairs of Players) Materials Needed: • scissors • tape • timer • Note: A parallelepiped is a six-sided figure with opposite sides parallel. A box is a parallelepiped with right-angled corners. 1. Print a copy of Master 8 Centimetre Grid Paper for each player. 2. Pairs of players choose a value for the surface area of a box that can be made using the grid paper, and tell their partner. 3. Start the timer. Working at the same time, the players have 5 min to • draw, cut out, and fold a box with the surface area chosen by their partner • prove that it is not possible to create a box with that surface area using the grid paper 4. At the end of 5 min, or earlier if both players agree, check the results. A player is awarded 1 point for a box that has been made correctly or for a valid argument that explains why it is not possible to make the box. 5. Play continues for as many rounds as players wish. The winner is the player with the highest score at the end of the game. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Clear the Fractions (2–4 Players) Materials Needed: • 1. Print and cut out the fraction cards on BLM: Fraction Cards. 2. Shuffle and deal eight fraction cards to each player. Place the rest face down in a pile. 3. Players inspect and arrange their cards. The object is to find groups of three fractions that are related by addition, subtraction, multiplication, or division. Example: 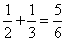 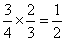 4. The first player examines the cards for as many groups of three cards as possible, and then places the groups on the table. If there are cards remaining in his or her hand, the player draws a card from the pile and the turn is over. Play moves to the next player on the left. 5. Play ends when • all the cards have been drawn from the pile, or • a player is able to place all of his or her cards on the table 6. The score for each player is 20 – n, where n is the number of cards remaining in a player’s hand at the end of the game. |
|
SE page 216 Information about provincial and territorial flags | ||
| Flags of the World | ||
| Provides an image and an overview of each provincial and territorial flag. Click on Protocol Order of Provincial/Territorial Flags and then click on each province or territory in the list. ( http://flagspot.net/flags/ca_prtcl.html ) |
||
| Worldflags101.com | ||
| Provides an image and information about the ratio of the width to the length of each flag. From the list on the left, click on each provincial or territorial flag. ( http://www.worldflags101.com/canada/alberta.aspx ) |
||
|
SE page 231 Information about Canada’s gold rushes and the life of Keish | ||
| Virtual Museum Canada | ||
| Profiles gold rush photographers who captured images that portray aspects of life in the Yukon during the Klondike Gold Rush. From the list on the right, click on Larss and Duclos for a portrait of Keish. ( http://www.virtualmuseum.ca/Exhibitions/Goldrushphoto/02english/02intro.html ) |
||
| Parks Canada | ||
| The National Historic Sites of Canada in the Klondike
Provides information about the Klondike Gold Rush. ( http://www.pc.gc.ca/lhn-nhs/yt/klondike/index_e.asp ) |
||
| Gold Rush Trail | ||
| Provides an extensive travel and history guide of the Gold Rush Trail, which connects Fort Langley, Cache Creek, Quesnel, Barkerville, and many British Columbia communities. Features maps and photos. ( http://www.goldrushtrail.net/indexgrt.asp ) |
||
| Barkerville Historic Town | ||
| From the list on the left, click on The History for historical information about Barkerville, the Gold Capital of British Columbia. Site also features information about local attractions and stage shows that re-enact the history of the region. ( http://www.barkerville.ca/newindex/index03.html ) |
||
| Virtual Museum Canada | ||
| Play the interactive Cariboo Gold Rush Adventure Game to find out more about the people, places, and events in the Cariboo Gold Rush of the 1860s. ( http://cariboogoldrush.entirety.ca/index.html ) |
||
| BC Heritage | ||
| Features resources about the Cariboo Gold Rush. Trace the Overlanders journey to the Cariboo Gold Rush. Check out primary source material from BC Archives, which includes journals, letters, and memoirs of the Cariboo Gold Rush era. ( http://bcheritage.ca/cariboo/contents.htm ) |
||
| The Centre for Canadian Studies at Mount Allison University | ||
| Features the history of the Canadian North West Mounted Police and their role in the Yukon Gold Rush. ( http://www.mta.ca/faculty/arts/canadian_studies/english/about/study_guide/nwmp/ ) |
||
|
SE page 239 Canada’s ecozones | ||
| The Green Lane™: Environment Canada | ||
| Provides an introduction to Canada’s ecozones. From the list on the left, choose Terrestrial Ecozones and then click on Map of Terrestrial Ecozones. On the map, click on each individual ecozone. Also from the list on the left, choose Marine Ecozones and then click on Map of Marine Ecozones. On the map, click on each individual ecozone. ( http://www.ec.gc.ca/soer-ree/English/vignettes/intro.cfm ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
The Prism Grill (3 or More Players) Materials Needed: • one 12-sided die • pencil and paper • calculator for checking calculations • timer 1. Players form a circular arrangement around a playing table and agree to a time limit, such as 20 min, for the game. 2. Player 1 rolls the die three times and notes the number that comes up each time. These numbers represent the base, height, and length of a right triangular prism. 3. After the third roll, • Player 1 uses pencil and paper to calculate the volume of the prism • Player 2 begins timing 4. As soon as Player 1 has an answer, • Player 2 stops timing and notes the elapsed time, t, in seconds • Player 3 checks the calculation and pronounces whether the answer is correct or not 5. Players receive 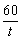 6. Play passes to Player 2. Player 3 times and Player 4 checks the answer. 7. The winner is the player with the highest score at the end of the time limit. Possible Variation: Roll the die twice. Let the numbers represent the radius and height of a right cylinder. |
|
SE page 252 The International Space Station | ||
| NASA | ||
| Provides information about the International Space Station. Click on active links for Interactives, ISS Science, Related Links, and Station Imagery. ( http://spaceflight.nasa.gov/station/ ) |
||
|
SE page 266 The Canadarm | ||
| The Shuttle Remote Manipulator System: The Canadarm | ||
| Provides information, a diagram, and photos of the Canadarm. ( http://www.ewh.ieee.org/reg/7/millennium/canadarm/canadarm_technical.html ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Zero to Hero (2–4 Players) Materials Needed: • deck of playing cards 1. Remove the jacks, queens, kings, and jokers from the deck of cards. • Aces count as 1s. • Red cards are positive. • Black cards are negative. 2. Take turns dealing the cards. Shuffle the cards and deal each player six cards. Place the remaining cards face down in a pile. 3. The object of the game is to assemble groups of cards that add to zero. There is no limit to the number of cards in a group, as long as the sum is zero. 4. The first player lays down a group of cards that add to zero, if there is one. If there are cards remaining in his or her hand, the player draws a card from the pile. Play passes to the next player to the left. 5. The round ends when all the cards in the pile have been drawn or a player has no more cards in his or her hand. 6. The score for each player is the sum of the value of the cards remaining in his/her hand. For the score, count all of the cards as positive. The winner is the player with the lowest score. 7. Play may proceed for as many rounds as the players wish. Keep a running total of the scores. |
|
SE page 302 Information about Aboriginal sources of Canadian place names | ||
| Indian and Northern Affairs Canada | ||
| Lists Aboriginal sources of Canada’s names of some provinces and territories and larger towns and cities. ( http://www.ainc-inac.gc.ca/pr/info/info106_e.html ) |
||
| Wikipedia® | ||
| Provides information about Aboriginal sources of Canada’s names of some provinces and territories and larger towns and cities. From the Contents list, click on active links for Provinces and Territories and then individual provinces and territories. ( http://en.wikipedia.org/wiki/List_of_place_names_in_Canada_of_Aboriginal_origin ) |
||
|
SE page 313 Information about the Ben Franklin and ROPOS submersibles | ||
| SUB-FIND.com | ||
| Includes a photo, a diagram, and information about the Ben Franklin. ( http://www.sub-find.com/historical.htm ) |
||
| NASA | ||
| This site was developed in support of collaborations with a number of educational activities.
Provides links to information about the Ben Franklin. ( http://seawifs.gsfc.nasa.gov/FRANKLIN/HTML/franklin_links.html ) |
||
| Vancouver Maritime Museum | ||
| Provides multimedia information about the Ben Franklin. From the list on the left, choose Virtual Tours and click on Ben Franklin. Choose from active links to History, Tour, Game, and Video. ( http://www.vancouvermaritimemuseum.com/ ) |
||
| ROPOS.com | ||
| Provides information about ROPOS submersibles. ( http://www.ropos.com ) |
||
|
SE page 317 Information about the modern pentathlon including the scoring system | ||
| Canadian Modern Pentathlon Association | ||
| Provides information about the pentathlon. For information about the scoring system for each event, click on shoot, fence. swim, ride, and run. ( http://www.pentathloncanada.ca ) |
||
| Modern-Pentathlon.com | ||
| Includes information about the pentathlon and the scoring system for each event. ( http://www.modern-pentathlon.com ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
It’s in the Cards (Pairs of Players) Materials Needed: • die • timer • 1. Print and cut out the cards on BLM: Linear Relation Cards. Shuffle and deal all of the cards to the two players. 2. Player 1 selects one of his or her cards and places it on the table. Player 2 rolls the die. The number represents a value of x. 3. Player 1 starts the timer. Player 2 has 10 s to determine the value of y by substituting the x-value into the linear relation on the card. 4. If the y-value is correct, Player 2 receives 5 points. 5. Play switches so that Player 2 selects a linear relation card and Player 1 rolls the die and solves for the y-value. 6. Play ends when all cards have been played. The winner is the player with the highest score. |
|
SE page 343 Practise graphing skills | ||
| Interactive Algebra | ||
| Provides graphing skills practice. Scroll down to Unit 3: Graphing. Try each of the four lessons. ( http://www.veazeys.com/math/lessons.htm ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Flip and Roll (Pairs of Players) Materials Needed: • two dice of different colours • one coin • timer 1. Player 1 rolls the dice and flips the coin. Heads represents an addition sign and tails represents a subtraction sign. 2. Player 1 starts the timer. Player 2 constructs a linear equation using the operation sign from the coin flip and the number values of the rolled dice. • The equation is x 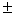 Player 2 solves for the variable. Example: x + 6 = 4 x = –2 3. If the solution is correct, Player 2 receives 60 – t points, where t is the time taken to solve the problem, in seconds. If it takes more than 60 s to solve the problem, award a score of zero, even if the solution is correct. 4. Play continues with players switching roles. 5. The game continues for as many rounds as the players wish. The winner is the player with the highest score at the end of the game. |
|
SE page 379 A Silly Putty® recipe | ||
| About.com: Chemistry | ||
| Provides two Silly Putty® recipes. ( http://chemistry.about.com/od/everydaychemistry/a/sillyputty_2.htm ) |
||
|
SE page 381 Practise solving linear equations using a balance scale | ||
| National Library of Virtual Manipulatives | ||
| Solve linear equations using a virtual balance scale. Use problems developed by the computer or the user. ( http://nlvm.usu.edu/en/nav/frames_asid_201_g_4_t_2.html?open=instructions ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Free Throw Contest (Any Number of Players) Materials Needed: • three pieces of 8.5 × 11 cardboard • counters or tokens for keeping score • ten plastic balls of diameter 4 cm or less • 1. Print and cut out the templates on BLM: Target Template. Use each template to draw a target hole centered on a piece of cardboard. The target holes are 6 cm, 9 cm, and 12 cm in diameter. 2. Each player receives 15 counters or tokens. The first player pays 3 counters to enter the game. 3. The player selects any one of the three targets. The target is placed at a distance calculated using the formula: Distance = 20 × diameter of hole (in cm). 4. The player tosses ten balls at the target, one at a time. For each ball that goes through the hole, the player receives 1 counter. 5. The next player continues the game. 6. The game ends when • one player runs out of counters, or • one player has 50 or more counters The winner is the player with the most counters. 7. Each player in a fair game has an equal chance of winning. Is this game fair? Explain. |
|
SE page 435 Try an on-line simulation | ||
| National Council of Teachers of Mathematics | ||
| Using a virtual spinner, change the number of sectors and increase or decrease their size to create any type of spinner. Follow the instructions to conduct a probability experiment by spinning the spinner many times. To start over, click New Experiment. ( http://illuminations.nctm.org/ActivityDetail.aspx?ID=79 ) |
||
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Napoleon’s Triangles (2–4 Players) Materials Needed: • coloured pencils or markers • scissors • 1. Print a copy of BLM: Napoleon’s Triangles. Shade each set of triangles a different colour. Cut out the triangles. 2. Place the START triangle on a flat surface. See #1 in the diagram. Divide the remaining triangles randomly and equally among the players. 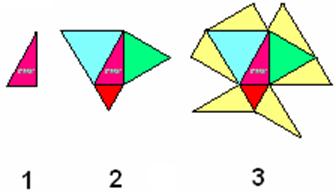 3. The first player places a triangle adjacent to one side of the START triangle. See #2 in the diagram. Play moves to the next player. 4. The players continue to take turns and build a tiling pattern similar to that shown in #3 of the diagram. Note: Two triangles of the same shape and size may not share a common side. 5. A player who cannot add a triangle skips a turn. 6. Play ends when • no player can make an allowable play • one player has used all of his or her triangles 7. The winner is the player with the fewest triangles left at the end of play. |
|
SE page 435 Try an on-line simulation | ||
| National Council of Teachers of Mathematics | ||
| Using a virtual spinner, change the number of sectors and increase or decrease their size to create any type of spinner. Follow the instructions to conduct a probability experiment by spinning the spinner many times. To start over, click New Experiment. ( http://illuminations.nctm.org/ActivityDetail.aspx?ID=79 ) |
||