
|
Use the links below to access a game for Chapter 5, along with related teaching notes. Games such as this one provide non-threatening practice for many students.
Chapter 5 Use the link below to access the materials needed to play the games in Chapter 7. Games such as these provide non-threatening practice for many students.
Chapter 7 Use the link below to access the materials needed to play the games in Chapter 9. Games such as these provide non-threatening practice for many students.
Chapter 9 Use the link below to access a game for Chapter 10. This game can provide challenging and non-threatening practice of the skills in Chapter 10.
Chapter 10 |
|
These lessons provided by Texas Instruments will focus on introducing you to the TI-83 Plus and TI-84 Plus through various guided interactive activities.
These lessons are provided through Texas Instruments, and as such do not necessarily follow the Western and Northern Canadian Protocol The Common Curriculum Framework for Grades K–9 Mathematics. The following lessons and activities align with our curriculum and standards and we hope you take the time to enjoy the module and take from it what you feel will apply in your classroom setting.
Module 6: Operations in Algebra: Rational Numbers and Expressions Module 9: Solving Linear Inequalities Module 17: Systems of Linear Equations To view these files, Adobe's free Flash Player application is required.
For additional support on this product and material please contact Texas Instruments.
For more exciting TI-83 Plus and TI-84 Plus modules, please visit the Texas Instruments site.
http://education.ti.com/educationportal/sites/US/nonProductMulti/pd_onlinealgebra_free.html If you have a TI-Navigator system, please visit the Texas Instruments site for supporting modules.
http://education.ti.com/educationportal/sites/US/nonProductMulti/pd_onlinemgnavigator_free.html The TI website offers a wide range of free activities for classroom use. Go to www.education.ti.com and visit the Activities Exchange portal for more resources that are aligned to Canadian standards.
* TI-83 Plus and TI-84 Plus are a trademark of Texas Instruments, Inc.
** TI-Navigator is a trademark of Texas Instruments, Inc. |
|
These lessons provided by Texas Instruments will focus on introducing you to the TI-Nspire handheld by looking at the layout of the keypad and the key features of operating the Applications.
These lessons will focus on introducing you to the TI-Nspire handheld by looking at the layout of the keypad and the key features of operating the Applications.
Lesson 1 Lesson 2 Lesson 3 Lesson 4 To view these files, Adobe's free Flash Player application is required.
Check out these exciting Texas Instruments web links:
Current TI online TI-NspireTM courses: http://education.ti.com/educationportal/sites/US/sectionHome/tutorials.html Current TI Online courses: http://education.ti.com/educationportal/sites/US/sectionHome/pd_onlinecourses_free.html Current Product Tutorials: http://education.ti.com/educationportal/sites/US/sectionHome/tutorials.html * TI-Nspire is a trademark of Texas Instruments, Inc.
|
| acute angle | An angle that is between 0° and 90°. |
||||||||
| angle of rotation (for symmetry) | The minimum size of the angle needed to turn a shape or design onto itself. The angle may be measured in degrees or fractions of a turn. (See page(s) 17) |
||||||||
| arc (of a circle) | A portion of the circumference of a circle. A minor arc is less than a semicircle, and a major arc is more than a semicircle.
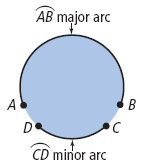 (See page(s) 378) |
||||||||
| area | The number of square units contained in a two-dimensional region. |
||||||||
| assumption | Something taken for granted, as though it were true. |
||||||||
| base (of a power) | number used as a factor for repeated multiplication. In 46, the base is 4. (See page(s) 93) |
||||||||
| biased sample | Does not represent the population, and can make survey results inaccurate. (See page(s) 431) |
||||||||
| binomial | An expression with two terms, such as 6y2 + 3 and 2x − 5y. |
||||||||
| bisect | Divide into two equal parts. |
||||||||
| bisector | A line or line segment that cuts an angle or line segment into two equal parts. 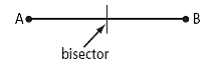 |
||||||||
| boundary point | The point that separates the values less than from the values greater than a specified value. If it is a possible value, it is shown with a closed circle on a number line. If it is not a possible value, the circle is open. For example, the boundary points for the inequality −4  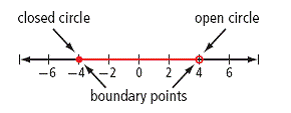 (See page(s) 342) |
||||||||
| central angle | An angle formed by two radii of a circle. The vertex of the angle is at the centre of the circle, and the endpoints are on the circle.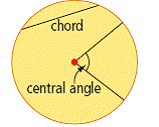 (See page(s) 378) |
||||||||
| centre of rotation | The point about which the rotation of an object or design turns. (See page(s) 16) |
||||||||
| chord | A line segment joining two points on the circumference of a circle. (See page(s) 378) |
||||||||
| circumference | The boundary of or distance around a circle. This is a linear measurement. It is often represented by the variable C. |
||||||||
| coefficient | See numerical coefficient. |
||||||||
| common denominator |
|
||||||||
| common multiple | A common multiple is a number that is a multiple of two or more numbers. For example, common multiples of 3 and 5 include 0, 15, and 30. |
||||||||
| composite object | An object made from two or more separate objects.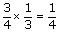 |
||||||||
| congruent | Identical in shape and size. |
||||||||
| constant | A known value in an equation or an expression. In the equation s = 3n − 2, −2 is a constant. |
||||||||
| convenience sample | A group of individuals that is chosen because its members are easy to access. |
||||||||
| coordinate grid | A grid made of intersecting vertical and horizontal lines. Also called a Cartesian plane. |
||||||||
| coordinate pair(s) | See coordinates. |
||||||||
| coordinate(s) | An ordered pair (x, y), is a pair of numbers used to locate a point on a coordinate grid. Coordinates are the values in an ordered pair. The x-coordinate is the distance from the vertical or y-axis. The y-coordinate in the distance from the horizontal or x-axis.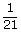 |
||||||||
| corresponding angles | Angles that have the same relative position in two geometric figures.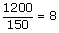 (See page(s) 146) |
||||||||
| corresponding sides | Sides that have the same relative position in two geometric figures. (See page(s) 146) |
||||||||
| degree of a polynomial | The degree of the highest degree term in a polynomial. For example, the polynomial 7a2 − 3a has a degree of two. (See page(s) 176) |
||||||||
| degree of a term | The sum of the exponents on the variables in a single term. For example, the degree of 3x3z2 is 5. A variable with no exponent has a degree of one. (See page(s) 176) |
||||||||
| diagonal | A line joining two non-adjacent vertices of a polygon.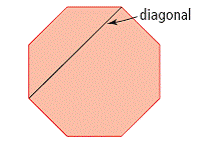 |
||||||||
| diameter | The distance across a circle through its centre. Represented by the variable d. |
||||||||
| distributive property | The rule that states a(b + c) = ab + ac for all real numbers a, b, and c. |
||||||||
| enlargement | An increase in the dimensions of an object by a constant factor. The enlargement can be 2-D or 3-D. (See page(s) 131) |
||||||||
| equation | A statement that two mathematical expressions are equal and have the same value. |
||||||||
| equilateral triangle | A triangle with three equal sides.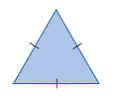 |
||||||||
| ethics | Involves judgments of right and wrong behaviour. For example, cheating on a test is wrong, or unethical. |
||||||||
| experimental probability | The probability of an event occurring based on experimental results. |
||||||||
| exponent | The number of times you multiply the base in a power by itself. For example, in 23, 3 is the exponent, so the base is multiplied by itself three times: 2 × 2 × 2 = 8. (See page(s) 93) |
||||||||
| exponential form | A shorter way of writing repeated multiplication, using a base and an exponent. For example, 5 × 5 × 5 in exponential form is 53. (See page(s) 93) |
||||||||
| extrapolate | To estimate a value beyond a given set of values. (See page(s) 223) |
||||||||
| generalize | To infer a general principle or make a broad statement from known facts. |
||||||||
| heptagon | A 2-D shape with seven sides. |
||||||||
| hypotenuse | side opposite the right angle in a right triangle.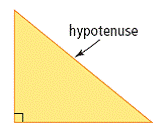 |
||||||||
| hypothesis | A proposition put forward to guide an investigation. |
||||||||
| inequality | A mathematical statement comparing expressions that may not be equal. These can be written using the symbols less than (<), greater than (>), less than or equal (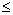 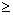 or not equal ( 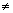 (See page(s) 341) |
||||||||
| inscribed angle | An angle formed by two chords that share a common endpoint. The vertex and endpoints are on the circle.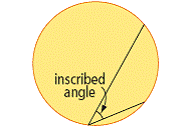 (See page(s) 378) |
||||||||
| interior angle | An angle that is formed inside a polygon by two sides meeting at a vertex.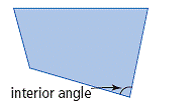 |
||||||||
| interpolate | To estimate the value between two given values. (See page(s) 222) |
||||||||
| isosceles triangle | A triangle with exactly two equal sides.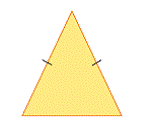 |
||||||||
| like terms | Terms that have the same variable(s) raised to the exponent(s). For example, 3x − 2x are like terms. (See page(s) 184) |
||||||||
| line of symmetry | A line running through the centre of an object or design such that the halves on each side of the line are mirror images. These lines can be vertical, horizontal, or oblique. A figure may have more than one line of symmetry. Also called a line of reflection.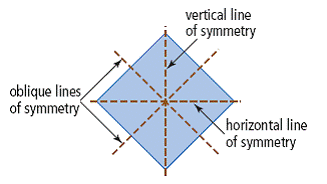 (See page(s) 6) |
||||||||
| linear equation | An equation whose graph is a straight line. |
||||||||
| linear relation | A relation that appears as a straight line when graphed. |
||||||||
| mean | A measure of central tendency calculated by finding the sum of a set of values divided by the number of values in the set. For example, for the set of values 6, 8, 5, 9, and 12, 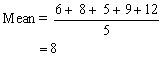 |
||||||||
| median | A measure of central tendency determined by the middle number in a set of data after the data have been arranged in order.
For the data 2, 5, 6, 8, and 9, the median is 6.
For the data 1, 3, 7, 7, 9, and 10, the median is 7. |
||||||||
| mode | A measure of central tendency determined by the most frequently occurring number in a set of data. There can be more that one mode.
For the data 3, 5, 7, 7, and 9, the mode is 7.
For the data 2, 2, 4, 6, 6, 8, and 11, the modes are 2, and 6. |
||||||||
| monomial |
|
||||||||
| non-perfect square | A rational number that cannot be expressed as the product of two rational factors. For example, you
(See page(s) 77) |
||||||||
| numerical coefficient | A number that multiplies the variable. In 3n − 2, the numerical coefficient is 3. |
||||||||
| oblique | Slanted, rather than vertical or horizontal. |
||||||||
| octagon | A 2-D shape with eight sides. |
||||||||
| opposite operation | Operations that “undo” other operations. Sometimes called “inverse operations.” Examples of opposite operations are addition and subtraction, multiplication and division, and squaring and taking the square root. |
||||||||
| opposites | Two numbers or expressions with the same numeral, but different signs. For example, +2 and −2, and 3x + 2 and −3x − 2, are opposites. |
||||||||
| order of operations | The correct sequence of steps for a calculation: Brackets, Exponents, Divide and Multiply in order from left to right, Add and Subtract in order from left to right. |
||||||||
| order of rotation | The number of times a shape or design fits onto itself in one turn. The order of rotation of this figure is 4.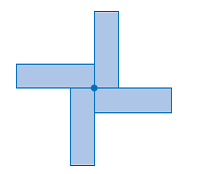 (See page(s) 17) |
||||||||
| parallegram | A four-sided figure with opposite sides that are parallel and equal in length.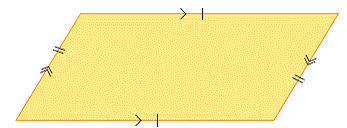 |
||||||||
| pentagon | A 2-D shape with five sides. |
||||||||
| perfect square | A number that is the product of two identical factors. 2 × 2 = 4, so 4 is a perfect square 6 × 6 = 36, so 36 is a perfect square |
||||||||
| perimeter | The distance around the outside of a two-dimensional shape or figure. |
||||||||
| perpendicular | Describes lines that intersect at right angles (90o).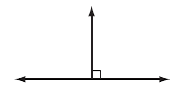 |
||||||||
| perpendicular bisector | A line that divides a line segment in half and is at right angles to it.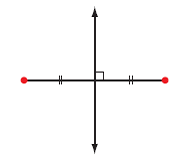 |
||||||||
| plane | A two-dimensional flat surface that extends in all directions. |
||||||||
| polygon | A two-dimensional closed figure made of three or more line segments. (See page(s) 154) |
||||||||
| polynomial | An algebraic expression formed by adding or subtracting terms. For example,
(See page(s) 175) |
||||||||
| population | All of the individuals that belong to a group being studied. (See page(s) 423) |
||||||||
| power | An expression made up of a base and an exponent. For example, for the power 63, 6 is the base and 3 is the exponent. (See page(s) 93) |
||||||||
| prime factorization | A number written as the product of its prime factors. For example, the prime factorization of 18 is 2 × 3 × 3. |
||||||||
| prime factors | Factors that are prime numbers. For example, the prime factors of 10 are 2 and 5. |
||||||||
| probability | The likelihood or chance of an event occurring. Probability can be expressed as a ratio, fraction, or percent. |
||||||||
| proportion | An equation that says that two ratios or two rates are equal. It can be written
|
||||||||
| Pythagorean relationship | The relationship between the lengths of the sides of a right triangle. The sum of the areas of the squares attached to the legs of the triangle equals the area of the square attached to the hypotenuse.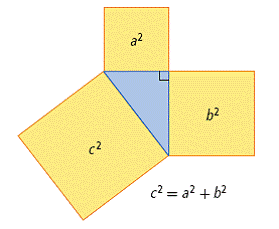 |
||||||||
| quadrilateral | A polygon that has four sides. |
||||||||
| radius | A line segment joining the centre of a circle to the outside edge. It can also refer to the length of this line segment and may be represented by the variable, r. |
||||||||
| random | An event in which every outcome has an equal chance of occurring. |
||||||||
| random sample | A sample of individuals chosen randomly from the whole population as a way of representing the whole population. Stratified samples and systematic samples are types of random samples. |
||||||||
| ratio | A comparison of two quantities with the same units. |
||||||||
| rational number | A number that can be expressed as the quotient of two integers, where the divisor is not zero.
(See page(s) 47) |
||||||||
| reciprocal | The multiplier of a number to give a product of 1. For example,
|
||||||||
| reduction | A decrease in the dimensions of an object by a constant factor. For example, in the diagram, the second bulb is half as large as the first. A reduction can be 2-D or 3-D. (See page(s) 133) |
||||||||
| regular polygon | A polygon with all sides equal and all interior angles equal. |
||||||||
| repeating decimal | A decimal number with a digit or group of digits that repeats forever.
|
||||||||
| right triangle | A triangle containing a 90o angle. |
||||||||
| rotation symmetry | Occurs when a shape or design can be turned about its centre of rotation so that it fits onto its outline more than once in a complete turn. The design in the figure fits onto itself 10 times in one turn. (See page(s) 16) |
||||||||
| sample | Any group of individuals selected from the population. (See page(s) 423) |
||||||||
| scale | A comparison between the actual size of an object and the size of its image. This can be expressed as a ratio, as a fraction, as a percent, in words, or in a diagram. For example, a scale of 1 cm : 50 km on a map means that 1 cm on the map represents 50 km. (See page(s) 139) |
||||||||
| scale diagram | A diagram that is similar to the actual figure or object. It may be smaller than or larger than the actual object, but must be in the same proportions. (See page(s) 140) |
||||||||
| scale factor | The constant factor by which all dimensions of an object are enlarged or reduced in a scale drawing. The dimensions of this rectangle is multiplied by 3 so the scale factor is 3. (See page(s) 132) |
||||||||
| similar figures | Figures that have the same shape, but different size. They have equal corresponding angles and proportional corresponding sides. (See page(s) 147) |
||||||||
| simulate | To create a model that reflects a particular situation. |
||||||||
| solution (of an inequality) | A value or set of values that result in a true statement. The solution can contain a specific value or many values. (See page(s) 353) |
||||||||
| square root | One of two equal factors of a number. The symbol is R. For example, 9 is the square root of 81 because 9 × 9 is 81. |
||||||||
| stratified sample | A sample that is created by dividing the whole population into distinct groups and then choosing the same fraction of members from each group. |
||||||||
| subtended |
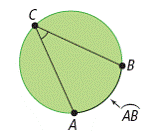 |
||||||||
| supplementary angles | Angles that add to 180o.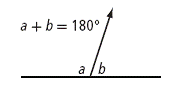 |
||||||||
| surface area | The number of square units needed to cover a 3-D object. The sum of the areas of all the faces of an object.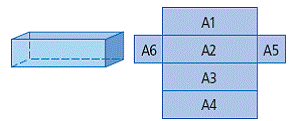 (See page(s) 26) |
||||||||
| survey | A question or questions asked of a sample of the population to gather opinions. |
||||||||
| symmetry | An object or image has symmetry if it is balanced and can fit onto itself either by reflection or rotation. (See page(s) 5) |
||||||||
| systematic sample | A sample created by choosing individuals at fixed intervals from an ordered list of the whole population. |
||||||||
| tangent (of a circle) | A line that touches a circle at exactly one point. The line is perpendicular to the radius at that point. The point where the line touches the circle is called the point of tangency.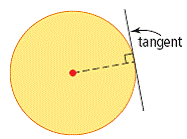 (See page(s) 394) |
||||||||
| term | A number or a variable, or the product of numbers and variables. The expression 5x + 3 has two terms: 5x and 3. (See page(s) 175) |
||||||||
| terminating decimal | A decimal number in which the digits stop. 0.4, 0.86, and 0.25 are terminating decimals. |
||||||||
| tessellation | A pattern or arrangement that covers an area or plane without overlapping or leaving gaps. Also called a tiling pattern.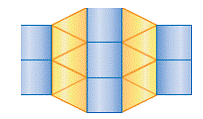 |
||||||||
| theoretical probability | The expected probability of an event occurring. The ratio of the number of expected favourable outcomes to the total number of possible outcomes for an event. |
||||||||
| transformation | A change in a figure that results in a different position or orientation. Examples are translations, reflections, and rotations. |
||||||||
| translation | A slide along a straight line.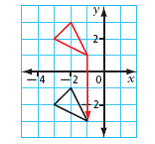 |
||||||||
| trapezoid | A quadrilateral with one pair of parallel sides.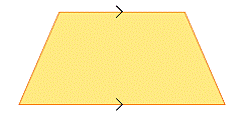 |
||||||||
| trinomial | A polynomial with three terms. x2 + 3x − 1 is a trinomial. |
||||||||
| variable | A letter that represents an unknown number. |
||||||||
| vertex | The point where two or more edges of a figure or object meet. The plural is vertices.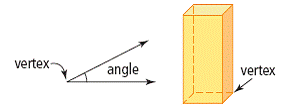 |
||||||||
| volume | The amount of space an object occupies. Measured in cubic units. |
||||||||
| voluntary response sample | A sample where the whole population is invited to participate. |
||||||||
|
Do you want to do better in math? We have some suggestions that will help you. Tips for StudentsWhy Studying Math is Different Take Charge and Take Action Preparing for Tests Why Studying Math is Different
|
|
Use this GSP applet to explore the Tech Link on page 153. Use this GSP applet as you complete the Explore in the Tech Link on page 385. Use this GSP applet to explore the Tech Link on page 393. This GSP applet will assist you with the Explore in the Tech Link on page 403. To extract the files from the zip folder, a software compression utility is required. A free evaluation version of Winzip is avalaible here.
|
|
Tetrical | ||
| http://www.tetrical.com/ | ||
| Use your knowledge of surface area to play Tetrical. Visualize how three-dimensional shapes they fit together to minimize surface area maximize your score. ( http://www.tetrical.com/ ) |
||
|
The Factor Game | ||
| http://illuminations.nctm.org/ActivityDetail.aspx?ID=12 | ||
|
The Factor Game allows you to brush up on factoring skills needed for a variety of mathematics topics, including fraction operations. ( http://illuminations.nctm.org/ActivityDetail.aspx?ID=12 ) |
||
|
Scaling Jigsaw | ||
| http://pbskids.org/cyberchase/games/sizeandscale/sizeandscale.html | ||
| This is a variant on the electronic jigsaw puzzle. Each piece must be scaled before it can be added to the puzzle. There is a time limit to determine the correct scale for each piece. ( http://pbskids.org/cyberchase/games/sizeandscale/sizeandscale.html ) |
||
|
Linear Lasers | ||
| http://mathforum.org/te/exchange/hosted/linearlasers/ | ||
| Polish your skills at visualizing linear relations in the context of a game. Given two targets, you must correctly construct the linear equation that will hit both targets. ( http://mathforum.org/te/exchange/hosted/linearlasers/ ) |
||
|
Lunar Lander | ||
| http://www.frontiernet.net/~imaging/lunar_lander_game.html | ||
|
Lunar Lander tests your ability to monitor rates of change while you bring a spacecraft to a safe landing before your fuel runs out. You can land on Earth, the moon, Mars, or Neptune to investigate the effects of different gravitational fields ( http://www.frontiernet.net/~imaging/lunar_lander_game.html ) |
||
|
The Monty Hall Game | ||
| http://math.ucsd.edu/~crypto/Monty/monty.html | ||
| This game requires you to make a selection then decide whether to switch your selection based on information provided by the computer. ( http://math.ucsd.edu/~crypto/Monty/monty.html ) |
||
|
The Nim Game | ||
| http://www.chlond.demon.co.uk/Nim.html | ||
| This is one of many versions of the Nim game. ( http://www.chlond.demon.co.uk/Nim.html ) |
||
|
The Chomp Game | ||
| http://lpcs.math.msu.su/~pentus/abacus.htm | ||
| In an unusual twist, the first step in this selection game requires you to deduce the rules. Once you have done so, you can play the game. Any number can play. ( http://lpcs.math.msu.su/~pentus/abacus.htm ) |
||
|
Logic Puzzles | ||
| http://www.math.uwaterloo.ca/navigation/ideas/Zeno/zenologic.shtml | ||
| This site offers a variety of classic logic puzzles, such as Who Owns the Zebra. ( http://www.math.uwaterloo.ca/navigation/ideas/Zeno/zenologic.shtml ) |
||
|
Rebus | ||
| http://kids.niehs.nih.gov/braintpics.htm | ||
| A rebus represents a phrase, such as
(head over heels)
You can find hundreds of rebus puzzles on this site, ranging from almost obvious to dazzlingly obscure. ( http://kids.niehs.nih.gov/braintpics.htm ) |
||
|
Place-It! | ||
| http://www.mathsisfun.com/games/place-it.html | ||
| This two-dimensional geometry game tests your spatial sense by requiring you to assemble a square from odd-shaped pieces. ( http://www.mathsisfun.com/games/place-it.html ) |
||
|
Tower of Hanoi | ||
| http://www.cut-the-knot.org/recurrence/hanoi.shtml | ||
| In this puzzle, a (variable) number of rings are placed in a "tower", largest to smallest. The object is to move the rings, one at a time, onto two additional towers, until all of the rings are on the last tower. ( http://www.cut-the-knot.org/recurrence/hanoi.shtml ) |
||
|
Hammurabi | ||
| http://maddrio.com/hammurabi/hammurabi.php | ||
| In this game, you are in charge of a kingdom for ten years and must make economic decisions each year of your reign. The objective is to finish your reign with your kingdom in better shape than when you started. ( http://maddrio.com/hammurabi/hammurabi.php ) |
||
|
Awari | ||
| http://www.copleys.com/awari.htm | ||
|
Awari is an ancient game that was played using stones and holes in the ground. The object is to capture the greatest number of stones. ( http://www.copleys.com/awari.htm ) |
||
|
Pentominoes | ||
| http://www.math.clemson.edu/~rsimms/java/pentominoes/ | ||
| Pentominoes a set of shapes, each made up of five squares. The challenge is to completely tile a section of the plane. Pentominoes can be rotated or flipped before being placed. ( http://www.math.clemson.edu/~rsimms/java/pentominoes/ ) |
||
|
The Chaos Game | ||
| http://math.bu.edu/DYSYS/applets/chaos-game.html | ||
|
The Chaos Game makes use of the Sierpinski Triangle and fractals to present a challenging puzzle. There are four levels of difficulty provided. ( http://math.bu.edu/DYSYS/applets/chaos-game.html ) |
||
|
The Game of Life | ||
| http://www.math.com/students/wonders/life/life.html | ||
| The Game of Life uses biological growth patterns and mathematical patterning to simulate the growth or death of a culture. The object is to create a living system that is able to sustain itself. ( http://www.math.com/students/wonders/life/life.html ) |
||
|
Hex-7 | ||
| http://www.mazeworks.com/hex7/index.htm | ||
|
Hex-7 is a strategy game that requires players to build a path across a playing surface made up of hexagons. ( http://www.mazeworks.com/hex7/index.htm ) |
||
|
Hare and Hounds | ||
| http://www.math.com/students/puzzles/hare/hare.html | ||
|
Hare and Hounds is a strategy game popular in 19th century. The hare must elude the hounds and escape. The hounds must trap the hare so that it cannot move. ( http://www.math.com/students/puzzles/hare/hare.html ) |
||
|
Rubik’s Cube | ||
| http://www.javaonthebrain.com/java/rubik/ | ||
| The Rubik’s Cube applet allows you to virtually manipulate a Rubik’s Cube in three dimensions. ( http://www.javaonthebrain.com/java/rubik/ ) |
||
|
Sudoku | ||
| http://www.websudoku.com/ | ||
|
Sudoku is a classic numbers game that requires you to complete a puzzle based on the numbers 1 to 9. ( http://www.websudoku.com/ ) |
||
|
The Hydra Game | ||
| http://math.andrej.com/2008/02/02/the-hydra-game/ | ||
| Every variation of this game has a solution. The object is to determine the solution in the least number of steps. ( http://math.andrej.com/2008/02/02/the-hydra-game/ ) |
||
| Body Surface Area Calculator |
||
| http://www.ultradrive.com/bsac.htm | ||
| This applet calculates the surface area of the human body given a height and mass. The formula can be viewed, and connected to exponents in chapter 3. ( http://www.ultradrive.com/bsac.htm ) |
||
| Surface Area Formulas |
||
| http://math.about.com/library/blmeasurement.htm | ||
| Visit this site for a quick summary or review of several useful surface area formulas, complete with detailed labeled diagrams. ( http://math.about.com/library/blmeasurement.htm ) |
||
| Fraction Calculator |
||
| http://www.helpingwithmath.com/resources/cal_fractions.htm | ||
| Check your answers to fraction problems. The online calculator can handle improper fractions, mixed numbers and whole numbers. All answers are expressed as mixed numbers in lowest terms. ( http://www.helpingwithmath.com/resources/cal_fractions.htm ) |
||
| Exponent Laws |
||
| http://www.curriculum.org/tcf/teachers/projects/algebra/exponentlaws.adp | ||
| This site provides good step-by-step explanations of the product of powers, quotient of powers, and power of a power exponent laws. ( http://www.curriculum.org/tcf/teachers/projects/algebra/exponentlaws.adp ) |
||
| Visual Scale Factor |
||
| http://www.learnalberta.ca/content/mejhm/html/video_interactives/rateRatioProportions/rat... | ||
| This is an interactive visual exploration of similar polygons, focusing on scale factors and proportions of sides. You can check your solutions online. ( http://www.learnalberta.ca/content/mejhm/html/video_interactives/rateRatioProportions/rat... ) |
||
| Polynomial Operations |
||
| http://math.about.com/od/polynomials/Polynomial_Help.htm | ||
| Need more practice working with polynomials? This site offers review tutorials along with practice adding, subtracting, multiplying and, dividing polynomials. Also available are online practice tests with instant feedback. ( http://math.about.com/od/polynomials/Polynomial_Help.htm ) |
||
| Pattern Generator |
||
| http://www.shodor.org/interactivate/activities/PatternGenerator/?version=1.6.0_13&browser... | ||
| Build your pattern recognition skills using this pattern generator. The difficulty level can be selected, and patterns consist of shapes and objects. Drag-and-drop to check your assessment of the pattern. ( http://www.shodor.org/interactivate/activities/PatternGenerator/?version=1.6.0_13&browser... ) |
||
| Virtual Algebra Tiles |
||
| http://my.hrw.com/math06_07/nsmedia/tools/Algebra_Tiles/Algebra_Tiles.html | ||
| Practice solving linear equations using virtual algebra tiles. You can choose to solve one-step or two-step equations. You can also work with equations that have variables on both sides. ( http://my.hrw.com/math06_07/nsmedia/tools/Algebra_Tiles/Algebra_Tiles.html ) |
||
| Solving Linear Inequalities |
||
| http://cnx.org/content/m19599/latest/ | ||
| This site compares solving linear inequalities in one variable to solving linear equations in one variable. Included are worked examples, including applications, and extra practice questions with available answers. ( http://cnx.org/content/m19599/latest/ ) |
||
| Dynamic Circle Geometry (Inscribed and Central Angles) |
||
| http://www.members.shaw.ca/ron.blond/Circle.Geom1.APPLET/index.html | ||
| Use this dynamic applet to explore and visualize circle geometry. Investigate the properties of inscribed and central angles by hanging the radius of a circle and by repositioning the circle vertically or horizontally. ( http://www.members.shaw.ca/ron.blond/Circle.Geom1.APPLET/index.html ) |
||
| Dynamic Circle Geometry (Tangents and Radii) |
||
| http://www.members.shaw.ca/ron.blond/Circle.Geom2.APPLET/index.html | ||
| Use this dynamic applet to explore and visualize circle geometry. Investigate how tangent lines relate to the radius of a circle. ( http://www.members.shaw.ca/ron.blond/Circle.Geom2.APPLET/index.html ) |
||
| Elections |
||
| http://www.sfu.ca/~aheard/elections/polls.html | ||
| This site provides information about Canadian federal election campaigns, the Canadian electoral system, polls, results from past federal elections, and tables of polling results. ( http://www.sfu.ca/~aheard/elections/polls.html ) |
||
| Statistics: Power from Data (Statistics Canada) |
||
| http://www.statcan.gc.ca/edu/power-pouvoir/toc-tdm/5214718-eng.htm | ||
| This site is a wonderful resource that addresses issues surrounding data collection, data analysis, and statistics. ( http://www.statcan.gc.ca/edu/power-pouvoir/toc-tdm/5214718-eng.htm ) |
||
| British Columbia Ministry of Education |
||
| http://www.bced.gov.bc.ca/students_ps.htm | ||
| The British Columbia Ministry of Education site is an excellent general source for information on education in British Columbia. ( http://www.bced.gov.bc.ca/students_ps.htm ) |
||
| Alberta Ministry of Education |
||
| http://ednet.edc.gov.ab.ca/students/ | ||
| The Alberta Ministry of Education site is an excellent general source for information on education in Alberta. ( http://ednet.edc.gov.ab.ca/students/ ) |
||
| Saskatchewan Ministry of Education |
||
| http://www.sasked.gov.sk.ca/ | ||
| The Saskatchewan Ministry of Education site is an excellent general source for information on education in Saskatchewan. ( http://www.sasked.gov.sk.ca/ ) |
||
| Manitoba Ministry of Education |
||
| http://www.edu.gov.mb.ca/ |
||
| The Manitoba Ministry of Education site is an excellent general source for information on education in Manitoba. ( http://www.edu.gov.mb.ca/ ) |
||
| Yukon Ministry of Education |
||
| http://www.education.gov.yk.ca/ | ||
| The Yukon Ministry of Education site is an excellent general source for information on education in the Yukon. ( http://www.education.gov.yk.ca/ ) |
||
| Northwest Territories Ministry of Education |
||
| http://www.gov.nt.ca/agendas/education/index.html | ||
| The Northwest Territories Ministry of Education site is an excellent general source for policy initiatives, curriculum, division of responsibilities and services, and other information on education in Northwest Territories. ( http://www.gov.nt.ca/agendas/education/index.html ) |
||
| Nunavut Ministry of Education |
||
| http://www.edu.gov.nu.ca/ |
||
| The Nunavut Ministry of Education site is an excellent general source for policy initiatives, curriculum, division of responsibilities and services, and other information on education in Nunavut. ( http://www.edu.gov.nu.ca/) |
||
| Math Central |
||
| http://mathcentral.uregina.ca/ | ||
| Math Central is an Internet service for mathematics teachers and students from kindergarten to grade twelve. Included on the site are a Resource Room containing shared resources and teaching ideas, the Teacher’s Bulletin Board, mathematics projects, a question-and-answer database, and a monthly mathematics problem. ( http://mathcentral.uregina.ca/ ) |
||
| Intermath Online Mathematics Dictionary |
||
| http://intermath.coe.uga.edu/dictnary/homepg.asp | ||
| The Intermath Online Mathematics Dictionary is a quick source for definitions of mathematical terms. Math terms are arranged alphabetically, with live hyperlinks for each letter of the alphabet. A search engine is included. ( http://intermath.coe.uga.edu/dictnary/homepg.asp ) |
||
| Learn Alberta Math Glossary |
||
| http://www.ronblond.com/MathGlossary/ | ||
| This site offers a glossary of mathematical terms organized by grade level. Also offered are interactive applets geared to the Western Protocol mathematics program. ( http://www.ronblond.com/MathGlossary/ ) |
||
| The Math Forum @ Drexel University |
||
| http://mathforum.org/ | ||
| The Math Forum at Drexel University (Philadelphia, Pennsylvania) is a comprehensive site for students and teachers of mathematics. It includes problems of the week and the popular Ask Dr. Math question-and-answer forum. ( http://mathforum.org/ ) |
||
| Mudd Math Fun Facts |
||
| http://www.math.hmc.edu/funfacts/ | ||
| This site contains hundreds of interesting mathematics facts useful for adding interest to projects. The facts are organized by topic (algebra, geometry, probability, etc). Famous problems (the Birthday problem, colouring pizza slices, Devil’s staircase, etc) are listed by name. ( http://www.math.hmc.edu/funfacts/ ) |
||
| Fun Math Lessons |
||
| http://math.rice.edu/~lanius/Lessons/ | ||
| Cynthia Lanius of Rice University (Houston, Texas) has created a number of mathematics lessons with an emphasis on having fun. Try them out. ( http://math.rice.edu/~lanius/Lessons/ ) |
||
| Figure This! Math Challenges |
||
| http://www.figurethis.org/index.html | ||
| This site contains a large number of mathematics challenges for you to enjoy and have fun with. ( http://www.figurethis.org/index.html ) |
||
| Coolmath 4 Kids |
||
| http://www.coolmath4kids.com/ | ||
| The Coolmath site includes interactive math games, puzzles, fractals, geometry, and other interesting activities for students at all levels of mathematics. Note: Because this is a commercially sponsored site, it includes advertising banners. ( http://www.coolmath4kids.com/ ) |
||
| Interactive Mathematics |
||
| http://www.cut-the-knot.org/content.shtml | ||
| This interactive site includes games and puzzles. Click on Games and Puzzles in the list on the left. ( http://www.cut-the-knot.org/content.shtml ) |
||
| Mensa Canada |
||
| http://www.canada.mensa.org/ | ||
| The Mensa Canada site offers a puzzle of the month (often mathematically-based), test questions that often use interesting patterns, and links to Mensa groups in other countries. ( http://www.canada.mensa.org/ ) |
||
| Homework Help |
||
| http://www.math.com/students/homeworkhelp.html | ||
| Need some help with your homework? This site offers worked examples, interactive self-quizzes, study tips, and test preparation, all organized by topics such as number sense, fractions, algebra, geometry, etc. ( http://www.math.com/students/homeworkhelp.html ) |
||
| Fermi Problems |
||
| http://mathforum.org/workshops/sum96/interdisc/sheila1.html | ||
| Looking for a fun way to practice estimation and real-world math? This library includes an explanation of what constitutes a Fermi problem, a short biography of Enrico Fermi, several worked examples, and a number of simple yet challenging Fermi questions. ( http://mathforum.org/workshops/sum96/interdisc/sheila1.html ) |
||
| Career Profiles |
||
| http://www.maa.org/careers/ |
||
| This site links to career profiles of people who use mathematics in their jobs every day. Included are short biographies, educational qualifications, and practical uses for mathematics in the career. (http://www.maa.org/careers/ ) |
||
| Math is Fun |
||
| http://www.mathisfun.com/ | ||
| This is a general site for all things mathematical. It includes games, puzzles, quizzes, worksheets, self-tests, nets for polyhedra, and many other items. ( http://www.mathisfun.com/ ) |
||
| MATHguide |
||
| http://www.mathguide.com/ | ||
| This site contains several resources for students, including the use of calculators, project ideas, and math puzzles. ( http://www.mathguide.com/ ) |
||
| Mathematrix |
||
| http://home.adelphi.edu/~stemkoski/mathematrix/index.html | ||
| Mathematrix explores mathematical recreation and draws from some of the lesser-known areas of mathematics. The activities are fun and interesting to anyone who enjoys puzzles and games. ( http://home.adelphi.edu/~stemkoski/mathematrix/index.html ) |
||
| A Dictionary of Units of Measurement |
||
| http://www.unc.edu/~rowlett/units/ | ||
| If you need a quick definition of any unit of measurement, or information on unit conversion, visit this site. Included are English, SI, and lesser-known measurement systems. ( http://www.unc.edu/~rowlett/units/ ) |
||
| Wolfram MathWorld |
||
| http://mathworld.wolfram.com/ | ||
| Wolfram MathWorld is an extensive general mathematics site for the serious learner. It includes interactive demonstrations, 3-D applets, worked examples, history of mathematics, terminology, and a wealth of other information. ( http://mathworld.wolfram.com/ ) |
||
| Math TV |
||
| http://www.mathtv.com/ | ||
| The Math TV site offers free video tutorials on a wide variety of math topics, including linear equations, exponents, polynomials, and inequalities. ( http://www.mathtv.com/ ) |
||
| Calculator Tutorials |
||
| http://education.ti.com/educationportal/sites/US/sectionHome/tutorials.html | ||
| Texas Instruments offers a comprehensive set of video tutorials for the TI-83/84 Plus family, the TI-89/89T family, the TI-NspireTM and the TI-NspireTM CAS. ( http://education.ti.com/educationportal/sites/US/sectionHome/tutorials.html ) |
||
| Select Math |
||
| http://www.boston.k12.ma.us/teach/technology/select/index.html | ||
| Students can use virtual manipulatives to explore concepts related to algebra (Algebra Alignments, Algebra II Alignments) and geometry (Geometry Alignments). Follow the links under Resources for access to other useful sites. ( http://www.boston.k12.ma.us/teach/technology/select/index.html ) |
||
Number |
Surface Area (cm2) |
|
1 cm |
16 |
16 |
2 cm |
9 |
36 |
3 cm |
4 |
36 |
4 cm |
1 |
16 |
Total Surface Area: |
104 |
The total surface area is 104 cm2.
'); }Chapter 1 Symmetry and Surface Area
Squares Everywhere

What is the sum of the surface areas of all of the squares?
The side length of the smallest squares measures 1 cm.
Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Tessellate Hexagons (2 Players) Materials Needed: • scissors • • 1. Print a copy of BLM: Tessellate Hexagons Game Board. Then, print and cut out the hexagons on a copy of BLM: Tessellate Hexagons. 2. Pairs of players choose either a set of lightly shaded or darkly shaded hexagons. 3. Player 1 places a hexagon anywhere on the game board so that its vertices line up with six dots. 4. Player 2 places a hexagon anywhere on the game board so that it tessellates with the first hexagon. This means that there are no overlaps or gaps. Player 2 records a score that is equal to the product of the values on the added hexagon and the values on any hexagons it touches. 5. Play continues until neither player can add a hexagon. 6. The winner is the player with the highest cumulative score. |
| SE page 2 Sampling of different places where symmetry can be found |
||
| AdrianBruce.com | ||
| Provides links to examples of line and rotation symmetry and includes animations and activities. ( http://www.adrianbruce.com/Symmetry ) |
||
| SE page 10 Explore symmetry |
||
| National Council of Teachers of Mathematics | ||
| Investigate mathematical properties of reflection or mirror symmetry. Provides links to lessons for describing reflections, relationships between reflections and symmetry, and reflections across two mirror lines. ( http://illuminations.nctm.org/LessonDetail.aspx?id=U139 ) |
||
| SE page 19 Examples of rotation symmetry |
||
| MathIsFun.com | ||
| Provides real world examples of rotation symmetry. ( http://www.mathsisfun.com/geometry/symmetry-rotational.html ) |
|
|
| |
||
| SE page 30 Information about how to calculate the surface area of different shapes |
||
| Math.com | ||
| Provides surface area formula for cube, prism, sphere, and cylinder. ( http://www.math.com/tables/geometry/surfareas.htm ) |
||
| SE page 32 Explore how surface area changes when a composite object is broken apart |
||
| NC State University | ||
| Use the animation to explore how the surface area of soil changes. ( http://courses.soil.ncsu.edu/resources/physics/texture/soilgeo.swf ) |
||
Chapter 2 Student Book
Student Book (PDF)
|
Chapter 2 Rational Numbers Oasis
Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Compare Ratios (2 or 4 Players) Materials Needed: • deck of playing cards • one six-sided die 1. Remove the kings from the deck of cards. • Aces count as 1s, jacks count as 11s, and queens count as 12s. • Other cards represent their face numbers. 2. Deal all of the cards equally to each player. 3. Each player rolls one die to decide who will play first. The player with the highest roll goes first. If there is a tie, roll again. 4. The first player rolls the die. Each player looks for cards that form a fraction closest to the number on the die. The player that has the closest ratio places the two cards that form the ratio on the table. In the case of a tie, all tied players place their cards on the table. Example: The number 4 is rolled. Ray has a queen and a 3 in his hand. This is the ratio 12 : 3. He puts the queen and the 3 on the table. 5. The other players check that the ratios on the table are correct. 6. Play moves to the next player. 7. The winner is the player who has no cards left. |
| SE page 42 Information about board games invented by Canadians |
||
| Wayne Kelly and Mr. Crokinole™ | ||
| Lists frequently asked questions and answers about crokinole. ( http://www.crokinole.com/faq.asp ) |
||
| Wikipedia® | ||
| Provides information about crokinole. From the Contents list, click on the links to Equipment, Gameplay, and History. ( http://en.wikipedia.org/wiki/Crokinole ) |
||
| About.com | ||
| Provides information about Trivial Pursuit, a game about general knowledge and popular culture. ( http://inventors.about.com/library/inventors/bl_trivia_pursuit.htm ) |
||
| Wikipedia® | ||
| Provides information about Trivial Pursuit. From the Contents list, click on the links to Gameplay and Editions. ( http://en.wikipedia.org/wiki/Trivial_Pursuit ) |
||
| Central Connector | ||
| Provides information about Balderdash, a game of bluffing and trivia. ( http://www.centralconnector.com/GAMES/balderdash.html ) |
||
| Wikipedia® | ||
| Provides information about Balderdash. From the Contents list, click on the links to Gameplay and Versions. ( http://en.wikipedia.org/wiki/Balderdash ) |
||
| High Game Enterprises | ||
| Provides information about Scruples, a game about ethical dilemmas. ( http://www.scruplesgame.com/main.html ) |
||
| Wikipedia® | ||
| Provides information about Scruples. ( http://en.wikipedia.org/wiki/Scruples_%28game%29 ) |
||
| BBC©MMIX | ||
| Provides information about Yahtzee, a dice game. ( http://www.bbc.co.uk/dna/h2g2/A3795663 ) |
||
| Wikipedia® | ||
| Provides information about Yahtzee. From the Contents list, click on the links to Rules overview and History. ( http://en.wikipedia.org/wiki/Yahtzee ) |
||
| SE page 49 Practise comparing and ordering solving rational numbers |
||
| ExploreLearning | ||
| Use the simulation to compare and order a rational number using an area model. Click on Launch Gizmo. ( http://www.explorelearning.com/index.cfm?method=cResource.dspDetail&ResourceID=300 ) |
||
| SE page 53 Learn about Neil Bartlett and research Canadian scientific discoveries |
||
| UC Berkeley | ||
| Provides information about Neil Bartlett. ( http://berkeley.edu/news/media/releases/2008/08/12_bartlett.shtml ) |
||
| Wikipedia® | ||
| Provides information about Neil Bartlett. From the Contents list, click on the links to Biography, Research, and Honors. ( http://en.wikipedia.org/wiki/Neil_Bartlett ) |
||
| GCS Research Society | ||
| Provides information about Canada’s greatest scientists and their achievements. Includes scientist profiles, science-based activities, and links to Canadian science-related web sites. ( http://www.science.ca ) |
||
| Canada Science and Technology Museum | ||
| Provides information and links to Canadian scientists, engineers, and innovators. ( http://www.sciencetech.technomuses.ca/english/about/hallfame/u_main_e.cfm ) |
||
| SE page 61 Prices of gas in Calgary, AB |
||
| GasBuddy Organization Inc. | ||
| Post and view recent retail gas prices in Calgary, AB. ( http://www.calgarygasprices.com/ ) |
||
| SE page 62 Information about Nunavut |
||
| Government of Nunavut | ||
| Provides information about Nunavut. ( http://www.gov.nu.ca/ ) |
||
| Wikipedia® | ||
| Provides information about Nunavut. From the Contents list, click on the links to Geography, History, Demographics, Economy, and People from Nunavut. ( http://en.wikipedia.org/wiki/Nunavut ) |
||
| SE page 63 Learn about Cindy Klassen and other Canadian speed skaters |
||
| Cindy Klassen: Official Site | ||
| Provides a biography of Cindi Klassen. ( http://www.cindyklassen.com) |
||
| Wikipedia® | ||
| Provides information about Cindy Klassen. From the Contents list, click on the links to Speed skating career and Results. ( http://en.wikipedia.org/wiki/Cindy_Klassen ) |
||
| Speed Skating Canada | ||
| Provides information about Canadian speed skating records. Click on the links to Long Track and Short Track. (http://www.speedskating.ca/results-ranking-and-records ) |
||
| Wikipedia® | ||
| Provides information about Canadian speed skaters. Click on the links to individual speed skaters. ( http://en.wikipedia.org/wiki/Category:Canadian_speed_skaters ) |
||
| SE page 81 Information about Heron of Alexandria |
||
| Technology Museum of Thessaloniki | ||
| Provides information about Heron of Alexandria. ( http://www.tmth.edu.gr/en/aet/5/55.html ) |
||
| Wikipedia® | ||
| Provides information about Heron of Alexandria. From the Contents list, click on the links to Background, Career, Inventions and achievements, and Mathematics. ( http://en.wikipedia.org/wiki/Hero_of_Alexandria ) |
||
| SE page 81 Learn about Sudoku puzzles |
||
| SudokuCentral.com | ||
| Provides information about the rules and history of Sudoku and strategies for solving, and includes online Sudoku puzzles. ( http://www.sudokucentral.com/what-is-sudoku ) |
||
| Wikipedia® | ||
| Provides information about Sudoku puzzles. From the Contents list, click on the links to History and Mathematics of Sudoku. ( http://en.wikipedia.org/wiki/Sudoku ) |
||
Chapter 3 Student Book
Student Book (PDF)
|
Chapter 3 Powers and Exponents Exponent Power You have four 3’s. Develop an expression using all four 3’s that is as large as possible when evaluated. Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Power Roll (Any Number of Players) Materials Needed: • scissors • two six-sided dice • 1. Print and cut out the cards on BLM: Power Roll Cards. Shuffle the cards. 2. Before playing the game, players decide whether to play for a certain length of time or for a certain number of rounds. 3. Each player rolls one die to decide who will play first. The player with the highest roll goes first. If there is a tie, roll again. 4. The first player draws a card from the pile and rolls the dice. The objective is to use one rolled number as the base and the other rolled number as the exponent to form a power that is equal to the number on the card. Each player gets 10 rolls to achieve this. Use the table to determine the scores.
Example: Sara’s card is 32. She rolls a 2 and a 5 on the fifth roll to form 25. Her score is 6 points. 5. Once a player forms an equivalent power or uses up all 10 rolls, play passes to the next player. 6. Play continues for as long as players wish. The winner is the player with the highest score. |
|
SE page 91 Learn about mobiles and how to create mobiles | ||
| National Gallery of Art, Washington | ||
| Use the virtual mobile maker to create a mobile, balance it, and view it in motion. ( http://www.nga.gov/education/classroom/interactive/mobile.htm ) |
||
| Zack Booth Simpson | ||
| Provides information about mobiles. Use the virtual mobile maker to create a mobile using beams and balls. ( http://www.mathcats.com/explore/virtual/mobile.html ) |
||
|
SE page 114 Information about the mountain pine beetle | ||
| Parks Canada | ||
| Provides information about the mountain pine beetle. From the list on the left, click on the links to Beetlemania, All about the beetle, Battle in the bark, History, Management, and Research. ( http://www.pc.gc.ca/docs/v-g/dpp-mpb/index_e.asp ) |
||
| Province of British Columbia | ||
| Provides information about the mountain pine beetle in BC. From the list, click on the links to Responding to the epidemic, Beetle biology, Contributing factors, and Infestation information. ( http://www.for.gov.bc.ca/hfp/mountain_pine_beetle/facts.htm ) |
||
| Government of Alberta | ||
| Lists frequently asked questions about the mountain pine beetle. ( http://www.srd.gov.ab.ca/forests/health/pestalerts/mpbfaq.aspx ) |
||
Chapter 4 Student Book
Student Book (PDF)
|
Chapter 4 Scale Factors and Similarity Pong Soccer Rachel held out a soccer ball and a ping pong ball from the window of a tall building such that their centres were at the same level. She dropped both balls at the same time and each fell straight down. Which ball will travel the farthest distance before hitting the ground? Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Similarity Challenge (1 Dealer and 2 Players) Materials Needed: • scissors • opaque paper bag • 1. Print and cut out the strips of varying lengths on BLM: Similarity Challenge Strips. Cut only on the solid lines; do not cut on the dotted lines. 2. Place the strips in a paper bag. Without looking at the contents of the bag, the dealer hands out eight strips to each player. 3. Each player constructs two similar figures using a scale factor other than 1. The similar figures may be triangles, quadrilaterals, or any other polygons. 4. If neither player can construct similar figures with the strips dealt, the dealer hands out two more strips to each player. Dealing continues until a player can construct similar figures. The successful player’s score is equal to 2n, where n equals the number of sides on each figure. 5. Return all strips to the bag and rotate play to a new dealer. 6. Play continues for at least two complete rounds of play. The winner is the player with the highest score. |
| SE page 126 Information about Douglas Cardinal and his designs |
||
| Canadian Museum of Civilization | ||
| Provides information about Douglas Cardinal and his designs, and a full tour of the Canadian Museum of Civilization, including a slide show and video clips. http://www.civilization.ca/cmc/exhibitions/cmc/architecture/tour09e.shtml( ) |
||
| Douglas Cardinal Architect Inc. | ||
| Provides biographical information about Douglas Cardinal and includes his portfolio and a slide show of his designs. ( http://www.djcarchitect.com/ ) |
||
| The Canadian Encyclopedia | ||
| Provides information about Douglas Cardinal and photos of his designs. ( http://www.thecanadianencyclopedia.com/index.cfm?PgNm=TCE&Params=A1ARTA0001394 ) |
||
| SE page 136 Explore enlargements and reductions of images graphically, numerically, or using a scale factor |
||
| The Concord Consortium | ||
| Use the virtual proportioner to manipulate images and compare their dimensions to the dimensions of other images. ( http://seeingmath.concord.org/resources_files/Proportioner.html ) |
||
| SE page 148 Learn about properties of similar triangles |
||
| Math Open Reference: This site was developed by John Page. | ||
| Provides information about the properties of similar triangles, including similar triangles that are rotations and reflections. Use the interactive tool to demonstrate similar triangles. ( http://www.mathopenref.com/similartriangles.html ) |
||
| SE page 155 Learn about properties of similar polygons |
||
| Math Open Reference: This site was developed by John Page. | ||
| Provides information about the properties of similar triangles and polygons, including similar polygons that are rotations and reflections. Use the interactive tool to demonstrate similar triangles. ( http://www.mathopenref.com/similarpolygons.html ) |
||
| SE page 157 Explore the changes when you manipulate two similar figures and vary the scale factor |
||
| ExploreLearning | ||
| Use the simulation to manipulate two similar polygons and vary the scale factor to see what changes are possible. Click on Launch Gizmo. ( http://www.explorelearning.com/index.cfm?method=cResource.dspDetail&ResourceID=195 ) |
||
Chapter 5 Student Book
Student Book (PDF)
|
Chapter 5 Introduction to Polynomials Polly Wolly Doodle Each of the letters a, b, c and d represents a single digit from 0 to 9. If cd – ab = bb, determine a possible value for each letter. Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Polynomial Sum or Difference (2 to 4 Players) Materials Needed: • scissors • 1. Print and cut out the cards on BLM: Sum or Difference Cards. 2. Shuffle the cards and deal eight cards to each player. Place the rest face-down in a pile. 3. Players inspect and arrange their cards. The object is to find groups of three expressions that are related by addition or subtraction. Examples: 2x + 3x = 5x or 8y – 3y = 5y Note: A wild card may be substituted for any term. 4. The first player places any three cards that are related as explained in step 3 on the table. If there are cards remaining in his or her hand, the player draws a card from the pile and the turn is over. 5. Play passes to the next player. Play ends when • all of the cards have been drawn from the pile, or • a player is able to place all of his or her cards on the table 6. Each player's score is 20 – n, where n is the number of cards remaining in the player’s hand. The winner is the player with the highest score. |
| SE page 170 Find at least 8 faces in the optical illusion |
||
| National Institute of Environmental Health Sciences | ||
| Find at least 8 faces in the optical illusion. ( http://kids.niehs.nih.gov/illusion/illusions21.htm ) |
||
| SE page 173 Try number puzzles |
||
| Mathematical Interactivities: This site was developed by David Hellam. | ||
| Use the interactive tool to try number puzzles. ( http://mathematics.hellam.net/maths2000/thinkno1.html ) |
||
| SE page 175 Information about the history of algebra |
||
| mathsisgoodforyou.com: This site was developed by Dr. Snezana Lawrence. | ||
| Provides information about the origin of the term algebra and al-Kwarizmi. Click on the link to al-Kwarizmi for biographical information. ( http://www.mathsisgoodforyou.com/topicsPages/algebra/name.htm ) |
||
| Algebra.com | ||
| Provides information about the history of algebra. Click on the link to al-Kwarizmi to learn about his contributions to algebra. ( http://www.algebra.com/algebra/about/history/ ) |
||
| SE page 177 Practise using virtual algebra tiles |
||
| Holt, Rinehart and Winston | ||
| Practise using virtual algebra tiles to model polynomials. ( http://my.hrw.com/math06_07/nsmedia/tools/Algebra_Tiles/Algebra_Tiles.html ) |
||
| SE page 182 Information about the Ironman Canada Triathlon and about the history of the Ironman competition |
||
| North America Sports | ||
| Provides information about the Ironman Canada Triathlon. Click on Information and then on Race history. ( http://www.ironman.ca/ ) |
||
| Wikipedia® | ||
| Provides information about the Ironman Triathlon organized by the World Triathlon Corporation. From the Contents list, click on History and Today. ( http://en.wikipedia.org/wiki/Ironman_Triathlon ) |
||
| SE page 186 Learn about the parts of a polynomial and combining like terms |
||
| Purplemath: This site was developed by Elizabeth Stapel. | ||
| Explains the basics of a typical polynomial. Click on Combining “like terms” for an explanation. ( http://www.purplemath.com/modules/polydefs.htm ) |
||
| West Texas A & M University: This site was developed by Kim Seward. | ||
| Defines term, coefficient, constant term, and polynomial, and explains monomials, binomials, and trinomials. Examples show how to find the degree of a given term. Scroll down to Combining Like Terms to learn how to combine like terms. ( http://www.wtamu.edu/academic/anns/mps/math/mathlab/beg_algebra/beg_alg_tut27_addpoly.htm ) |
||
| SE page 194 Learn about adding and subtracting polynomials |
||
| West Texas A & M University: This site was developed by Kim Seward. | ||
| Provides a lesson about adding and subtracting polynomials. Scroll down to Adding Polynomials and to Subtracting Polynomials. Then, scroll down to Practice Problems 3a – 3b. ( http://www.wtamu.edu/academic/anns/mps/math/mathlab/beg_algebra/beg_alg_tut27_addpoly.htm ) |
||
| Regentsprep.org: This site was developed by Donna Roberts. | ||
| Provides a lesson on adding and subtracting polynomials and practice problems. Also, demonstrates using algebra tiles to model solutions. Click on the links in the list of Resource Titles. (http://www.regentsprep.org/Regents/math/ALGEBRA/AV2/indexAV2.htm ) |
||
| |
||
| Purplemath: This site was developed by Elizabeth Stapel. | ||
| Provides a lesson on adding polynomials. At the top of the page, click on Subtracting polynomials for a lesson on subtracting polynomials. ( http://www.purplemath.com/modules/polyadd.htm ) |
||
Chapter 6 Student Book
Student Book (PDF)
|
Chapter 6 Linear Relations Pattern Puzzle Each row in this table of numbers uses the same pattern. What is the missing number?
Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Three Card Line (2 or 4 Players) Materials Needed: • deck of playing cards • timer 1. Remove the face cards from the deck of cards, such that only the ace through 10 of each suit remains. • Aces count as 1s. • Red cards are positive. • Black cards are negative. 2. Take turns dealing the cards. Shuffle the cards and place them face down in a pile. 3. Player 1 draws three cards. Using the equation y = ax + b, let the first card represent the value of a, the second card represent the value of x, and the third card represent the value of b. Player 2 starts the timer. Player 1 has 10 s to determine the value of y using the values of the three cards. If the y value is correct, the player is awarded 1 point. 4. Play moves to the next player. 5. Play ends when there are less than three cards in the pile. The winner is the player with the highest score. |
| SE page 209 Information about supertankers and other oil tankers |
||
| Wikipedia® | ||
| Provides information about oil tankers, including photos and diagrams. ( http://en.wikipedia.org/wiki/Oil_tanker ) |
||
| SE page 230 Learn about the Intertropical Convergence Zone (ITCZ) |
||
| NASA | ||
| Provides information about the ITCZ, including a photo. ( http://earthobservatory.nasa.gov/IOTD/view.php?id=703 ) |
||
| University of South Carolina: Site developed by Greg Carbone. | ||
| Animation shows how the seasonal migration of the ITCZ in Africa affects seasonal precipitation patterns. ( http://people.cas.sc.edu/carbone/modules/mods4car/africa-itcz/index.html ) |
||
| Wikipedia® | ||
| Provides information about the ITCZ. From the Contents list, click on the links to Position and Effects on weather. ( http://en.wikipedia.org/wiki/Intertropical_convergence_zone ) |
||
| SE page 239 Practice matching graphs and linear equations |
||
| Quia Web | ||
| Match the linear graphs to their equations by clicking one item and then clicking its corresponding match. If the match is correct, the two items will be turned over. If the match is incorrect, the two items will remain the same. ( http://www.quia.com/mc/276756.html ) |
||
| SE page 241 Learn about using a graphing calculator to enter data on a table and plot the data on a graph |
||
| BLM 6–9 Method 3: Use a Graphing Calculator | ||
| Demonstrates using a graphing calculator to enter data on a table and plot the data on a graph. ( ../../school/secondary/mathlinks/docs/mhr_ml9_se_BLM_6_9.pdf ) |
||
| MathBits.com | ||
| Demonstrates using a TI-83 +/ 84 graphing calculator to solve algebraic equations and plot the data on a graph. View Example 1. ( http://www.mathbits.com/MathBits/TISection/Algebra1/SolveEquations.htm ) |
||
| SE page 248 Information about hot-air balloon records |
||
| Fédération Aéronautique Internationale | ||
| Provides information about current balloon records including altitude, distance, duration, and shortest time around the world. Scroll down to Current Balloon Records and click on List of Absolute Records. ( http://records.fai.org/balloons/ ) |
||
Chapter 7 Student Book
Student Book (PDF)
|
Chapter 7 Multiplying and Dividing Polynomials Magic Polynomials A polynomial consists of powers of x. All the numerical coefficients are single digits from 0 to 9. If x = 10, the value of the polynomial is 2351. What is the polynomial? Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Polynomial Product or Quotient (2 to 4 Players) Materials Needed: • scissors • 1. Print and cut out the cards on BLM: Product or Quotient Cards. 2. Shuffle the cards and deal eight cards to each player. Place the rest face down in a pile. 3. Players inspect and arrange their cards. The object is to find groups of three expressions that are related by multiplication or division. Examples: 2x × 3y = 6xyor 8xy ÷ 4y = 2x Note: A wild card may be substituted for any term. 4. The first player places any three cards that are related as explained in step 3 on the table. If there are cards remaining in his or her hand, the player draws a card from the pile and the turn is over. 5. Play passes to the next player. Play ends when • all of the cards have been drawn from the pile, or • a player is able to place all of his or her cards on the table 6. Each player's score is 20 – n, where n is the number of cards remaining in the player’s hand. The winner is the player with the highest score. |
Chapter 8 Student Book
Student Book (PDF)
|
Chapter 8 Solving Linear Equations DaVinci Goes Linear A code is based on the linear equation y = x + 3. Assign a number to each letter in the alphabet. Calculate the corresponding value of y, and use it to replace the letter in a message. For example, if C is letter 3, the corresponding value of y is 6. So C becomes an F. To decode a message, reverse the process. What message does the code PHHWDWVLA indicate? Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
It’s All in the Cards (2 Players) Materials Needed: • deck of playing cards • timer 1. Remove the kings from the deck of cards. • Aces count as 1s, jacks count as 11s, and queens count as 12s. • Red cards are positive. • Black cards are negative. 2. Take turns dealing the cards. Shuffle the cards and place them face down in a pile. 3. Player 1 draws four cards. Using the equation ax + b = cx + d, let the cards represent the values of a, b, c, and d, in order, as they are drawn. Player 2 starts the timer. Player 1 has 20 s to determine the value of x using the values of the four cards. If the value is correct, the player is awarded 5 points. 4. Play moves to Player 2. 5. Play ends when there are less than four cards in the pile. The winner is the player with the highest score. |
| SE page 288 Information about Canada’s Food Guide and how to use the food guide, such as Eating Well with Canada’s Food Guide and Eating Well with Canada’s Food Guide –First Nations, Inuit and Métis |
||
| Health Canada | ||
| Provides information about Canada’s Food Guide. Click on the links to Food Guide Basics, Choosing Foods, Using the Food Guide, and Maintaining Healthy Habits. Build your own Food Guide by clicking on Create My Food Guide. For more information, click on Educators and Communicators, and Food Guide for First Nations, Inuit and Métis. ( http://www.hc-sc.gc.ca/fn-an/food-guide-aliment/index-eng.php ) |
||
| SE page 291 Learn about nutrition, healthy eating, and the nutritional values of different foods |
||
| Health Canada | ||
| Provides information about nutrition and healthy eating. Scroll down and click on the links listed in the Food and Nutrition Features for information about Bottled Water, Nutrition Labelling, Chemical Contaminants, and Food Allergies and Intolerances. ( http://www.hc-sc.gc.ca/fn-an/index-eng.php ) |
||
| Health Canada | ||
| Provides information about nutrient values of some common foods that are organized by category. ( http://www.hc-sc.gc.ca/fn-an/alt_formats/hpfb-dgpsa/pdf/nutrition/nvscf-vnqau-eng.pdf ) |
||
| Nutri-facts.com | ||
| Provides information about nutritional values of different foods. Enter keywords to search the food label database. ( http://www.nutri-facts.com/index.php ) |
||
| Dietitians of Canada | ||
| Provides information about nutrition and healthy eating. From the menu on the left, click on Eat Well, Live Well and then on the links that appear. ( http://www.dietitians.ca/ ) |
||
| NutritionData.com | ||
| Provides information about nutrition and healthy eating and a nutrient search tool. On the menu bar at the top, click on the links that appear for Tools and Topics. ( http://www.nutritiondata.com/ ) |
||
| SE page 292 Learn about Steve Nash’s life, his career, and his work in communities |
||
| JockBio.com | ||
| Provides biography of Steve Nash. On the menu bar, click on Facts for a summary of his life and achievements. ( http://jockbio.com/Bios/Nash/Nash_bio.html ) |
||
| Canada Basketball Official Site | ||
| Provides statistics and career highlights of Steve Nash. ( http://www.basketball.ca/en/hm/inside.php?sid=186&id=1677 ) |
||
| stevenash.org | ||
| Provides information about the Steve Nash Foundation set up to assist underserved children. On the menu, click on About Us and then on About the Foundation. ( https://stevenash.org/ ) |
||
| SE page 304 Learn about waterfalls around the world |
||
| State Geological Service of Latvia: This site was developed by Gatis Pavils. | ||
| Provides information and photos of the highest waterfalls in the world. ( http://mapx.map.vgd.gov.lv/geo3/Ukr/Pamatlapas_Slices/Arzemes_E/Pasaules%20augstakie_E.htm ) |
||
| SE page 322 Learn about the speed of different animals |
||
| WiseGEEK.com | ||
| Provides information about fastest land animals, fastest water animals, and fastest air animals. ( http://www.wisegeek.com/what-are-the-fastest-animals-in-the-world.htm ) |
||
| Quia Web | ||
| Uncover the hidden picture by putting the animals in order of speed. Enter the numbers 1 to 10 in the fields provided. ( http://www.quia.com/pp/21925.html ) |
||
Chapter 9 Student Book
Student Book (PDF)
| '+ ' | Costx | '+
'
Anwar | '+
'x – 15 | '+
'
Grace | '+
'x – 14 | '+
'
Colin | '+
'x – 13 | '+
'
Diana | '+
'x – 12 | '+
'
Evan | '+
'x – 11 | '+
'
The cost of the present must be greater than the total amount of dollars of the five friends.
'+ 'x > x – 15 + x – 14 + x – 13 + x – 12 + x – 11
'+ 'x > 5x – 65
'+ 'x < 16.25
'+ 'Since Anwar is $15 short, x > 15. The only integer that satisfies both '+ 'inequalities is 16. Therefore, the present cost $16.
'); }Chapter 9 Linear Inequalities

It is Damian’s birthday. His friends Anwar, Grace, Colin, Diana, and Evan went to the store to buy a present. Each had an integral number of dollars. They found a suitable item whose price was an integer. Anwar was $15 short, Graeme was $14 short, Colin was $13 short, Dieter was $12 short, and Ewan was $11 short. Even when they pooled all of their funds, they could not buy the item. What was the cost of the item?
Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown.
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Spin2 Flip (2 Players) Materials Needed: • scissors • two paper clips • two pencils • coin • timer • 1. Print and cut out the spinners on BLM: Spin2 Flip Spinners. Use a pencil and paper clip to complete each spinner. • Numbers on unshaded sectors are positive. • Numbers on shaded sectors are negative. 2. Player 2 spins both spinners, flips the coin, and then starts the timer. Player 1 develops an inequality using the two numbers spun and the coin flip as follows: Heads: x ± Spinner 1 > Spinner 2 Tails: x ± Spinner 1 < Spinner 2 Example: Megan spins a 6 on Spinner 1 and a –4 on Spinner 2, and flips tails. The inequality is x + 6 < –4. 3. Player 1 has 10 s to develop and solve the inequality. If the solution is correct, the player is awarded 2 points. 4. Play moves to Player 2. 5. The winner is the first player to score 20 points by the end of a round. |
|
SE page 339 Information about the history of Ferris wheels and the tallest ones in the world | ||
| About.com | ||
| Provides information about George Ferris and his invention of the first Ferris wheel. ( http://inventors.about.com/library/inventors/blrollercoaster.htm ) |
||
| Illinois Institute of Technology: Paul V. Galvin Library Digital History Collection | ||
| Provides information about the first Ferris Wheel. ( http://columbus.iit.edu/dreamcity/00024024.html ) |
||
| Wikipedia® | ||
| Provides information about the history of Ferris wheels and the tallest ones in the world. From the Contents list, click on the links to History and World’s tallest Ferris wheel installations. ( http://en.wikipedia.org/wiki/Ferris_wheel ) |
||
|
SE page 363 Practise solving inequalities using multiplication and division | ||
| Explorelearning | ||
| Solve an inequality by multiplying or dividing both sides. Examine the inequality on a number line and determine which points are solutions for the inequality. ( http://www.explorelearning.com/index.cfm?method=cResource.dspView&ResourceID=273 ) |
||
|
SE page 366 Learn how to solve inequalities using a graphing calculator | ||
| MathBits.com | ||
| Demonstrates using a TI-83 +/ 84 graphing calculator to solve linear equalities and graph a solution set. ( http://mathbits.com/MathBits/TISection/Algebra1/linearinequ.htm ) |
||
Chapter 10 Student Book
Student Book (PDF)
|
Chapter 10 Circle Geometry
Allan tied a ball to a string and whirled it around in a circular path, as shown. He let go of the string when the ball was at point P. Which of his friends is most likely to catch the ball? Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Roll and Draw (2 Players) Materials Needed: • one six-sided die • timer 1. Each player rolls the die. The player with the highest roll begins. 2. Player 1 rolls the die and starts the timer. • The player uses the number rolled to divide a circle into equal parts and then calculates the central angle. Example: Eli rolls a 2. He calculates the central angle that is formed from dividing a circle into two equal parts. • The player sketches the circle and labels the central angle. Player 2 stops the timer and records the score, which is the number of seconds that have elapsed. 3. Play moves to Player 2. 4. Play continues until a player reaches 200 points. The winner is the player with the lowest score. |
| SE page 374 Information about Euclid |
||
| mathsisgoodforyou.com | ||
| Provides biographical information about Euclid. Click on the link to Elements for information and visuals about Euclid’s book. ( http://www.mathsisgoodforyou.com/people/euclid.htm ) |
||
| Clark University: This site was developed by D.E. Joyce. | ||
| Use the interactive geometry applet to learn about Euclid’s Elements. ( http://aleph0.clarku.edu/~djoyce/java/elements/elements.html ) |
||
| SE page 379 Explore geometric properties of angles in a circle on a geoboard or a computer |
||
| National Library of Virtual Manipulatives | ||
| Explore geometric properties of central angles and inscribed angles in a circle using a virtual geoboard. ( http://nlvm.usu.edu/en/nav/frames_asid_285_g_4_t_3.html?open=activities&from=category_g_4... ) |
||
| |
||
| |
||
| SE page 386 Explore geometric properties of perpendicular bisectors to a chord on a computer |
||
| Argyll Home Education Services Centre: This site was developed by Jim Reed. | ||
| Use the interactive activity to explore the pattern for perpendicular bisectors to a chord. Then, watch the animation to check for understanding. ( http://argyll.epsb.ca/jreed/math20p/circles/chordBisector.htm ) |
||
| SE page 393 Information about sand mandalas |
||
| Cornell University | ||
| Provides information about sand mandalas and photos. ( http://www.graphics.cornell.edu/online/mandala/ ) |
||
| SE page 394 Explore geometric properties of tangents to a circle on a computer |
||
| Argyll Home Education Services Centre: This site was developed by Jim Reed. | ||
| Use the interactive activities to explore the properties of tangents to a circle. Then, watch the animations to check for understanding. ( http://argyll.epsb.ca/jreed/math20p/circles/tangent.htm ) |
||
|
Chapter 11 Data Analysis Deserted Island
Note: Brain teasers are often open to more than one interpretation, and multiple answers may be possible. Sample solutions are shown. |
|
Want a fun way to test your knowledge of math terms? Try this Crossword Puzzle and see how many you can get!
|
|
Licence Plates (Any Number of Players) Materials Needed: • chips or tokens of two colours 1. The object is for players to observe licence plates on motor vehicles in a parking lot and note the last two numbers on each plate. They continue to observe licence plates until a match is found or they note 20 licence plates. This completes a round of play. Before doing so, each player makes a prediction about whether or not there will be a match. 2. One player acts as the bank and distributes five chips of the appropriate colour to each player. • Players who predict there will be a match get chips of one colour. • Players who predict there will not be a match get chips of another colour. Players play against the bank. 3. The winners in a round receive a chip. The losers must pay a chip. 4. Play at least six rounds. 5. Determine which prediction is more likely to win. |
| SE page 413 Information about national parks |
||
| Parks Canada | ||
| Provides information about the national parks of Canada. From the list on the left, click on Find a National Park. Click on the names of the parks. ( http://www.pc.gc.ca/progs/np-pn/index_E.asp ) |
||
| Kanada News™ | ||
| Provides information about the national parks of Canada by province or territory. ( http://www.national-parks-canada.com/ ) |
||
| SE page 431 Information about gene types that determine eye colour |
||
| Athro Limited: This site was developed by Paul Morris and Susan Morris. | ||
| Provides information about how eye colour is inherited. Use the interactive eye colour calculator to determine eye colour and then click on the link that explains how human eye colours are inherited. ( http://www.athro.com/evo/inherit.html ) |
||
| SE page 437 Information about road safety and risk factors, and factors affecting car insurance rates |
||
| Transport Canada | ||
| Provides information about road and motor vehicle safety. Click on the links related to road and motor vehicle safety listed below Road Transportation. ( http://www.tc.gc.ca/eng/roadsafety/menu.htm ) |
||
| Insurance Bureau of Canada | ||
| Provides information about factors affecting car insurance rates. ( http://www.ibc.ca/en/Car_Insurance/Introduction/How_Auto_Rates_Calculated.asp ) |
||
| SE page 448 Environment Canada’s climate data for locations and dates to 1840 |
||
| Environment Canada | ||
| Provides climate data for specific locations and dates going back to 1840. ( http://www.climate.weatheroffice.ec.gc.ca/climateData/canada_e.html ) |
||
| SE page 449 Sources of online headlines |
||
| CBC/Radio Canada | ||
| Provides headlines. ( http://www.cbc.ca/news/ ) |
||
| BBC©MMIX | ||
| Provides headlines. ( http://news.bbc.co.uk/ ) |
||
| Scholastic Inc. | ||
| Provides headlines. ( http://www2.scholastic.com/browse/scholasticNews.jsp?FromBrowseMod=true&Ns=Pub_Date_Sort|... ) |
||
| Student News Net and Encyclopaedia Britannica | ||
| Provides headlines. ( http://www.studentnewsnet.com/ ) |
||
| SE page 449 Sources of online newspapers |
||
| Homer.ca | ||
| Provides links to newspapers from British Columbia, Alberta, Saskatchewan, and Manitoba. ( http://homer.ca/newspapers/western.htm ) |
||
| Web Wombat Pty Ltd. | ||
| Provides links to Canadian newspapers. ( http://www.onlinenewspapers.com/canada.htm ) |
||